АЛГЕБРА!
Решить неравенство.
С решением и объяснением х² ≤ 3 - 4х
Другие вопросы по теме Алгебра
Популярные вопросы
- Как ты думаешь,почему во многих учебниках языка обычно сначало...
1 - Написать текст немение сто слов с 5 количественными,2 порядковыми...
1 - Первая машина проходит за час 38 км.а вторая 43 км.эти машины...
1 - Сочинение к картине ф. васильева мокрый луг....
2 - Написать план по тему музыкальная драмматургия...
1 - Какая точка земли имеет нулевые координаты...
2 - Вкаком слове (или словах) можно выделить окончание: меню. ёлка....
1 - Какое проверочное слово к слову полотенце (проверить первую...
1 - Найдите однокоренные слова корова коровы дуб дубовый сосна сосны...
3 - Вкакой ситуации можно применить пословицу удачливый еще не герой...
3
ответ: x ∈ (-∞;1]∪[3;+∞)
-x^2 ≤ 3 - 4x
4x - x^2 - 3 ≤ 0
-x^2 + 4x - 3 ≤ 0 |-1
x^2 - 4x + 3 ≥ 0
x^2 - 4x + 3 = 0
D = b^2 - 4ac = 16 - 12 = 4
x1,2 = (-b +/-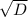 )/2a
)/2a
x1 = (4 + 2)/2 = 3
x2 = (4 - 2)/2 = 1
Построение на картинке
-x² ≤ 3 - 4x⇒x²-4x+3≥0
По Виету х=3;х=1
Решим неравенство методом интервалов.
13
+ - +
х∈(-∞;1]∪[3;+∞)