Алгебра
номер 7.77 под номером 1 и 3
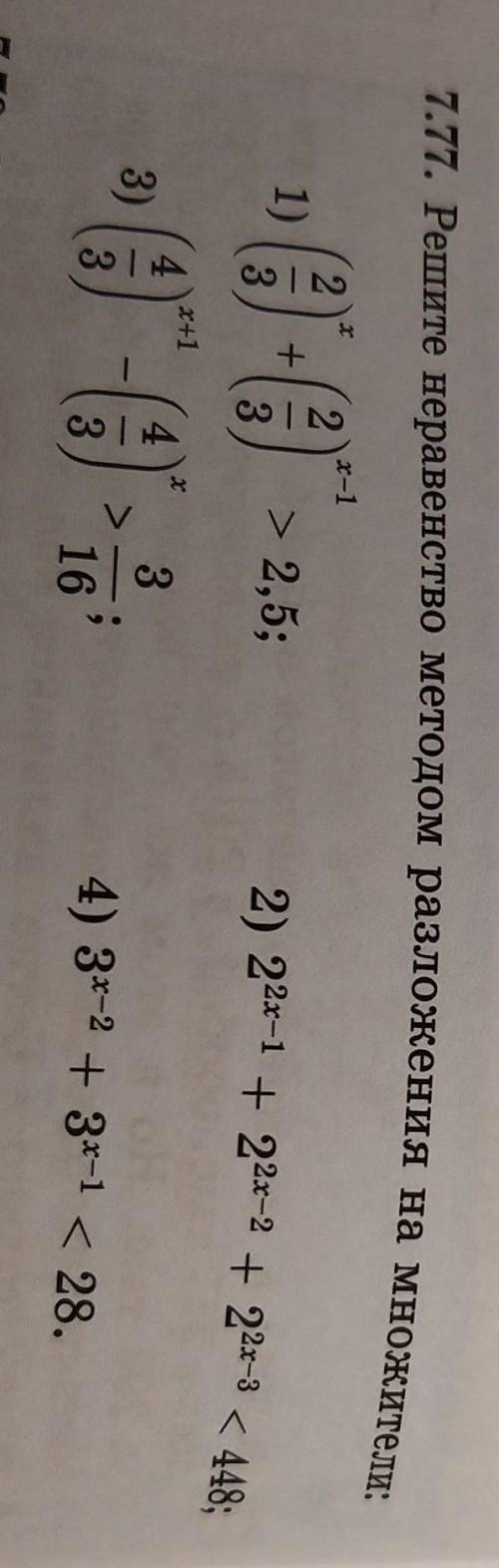
Другие вопросы по теме Алгебра
Популярные вопросы
- 1- mashq. Berilgan rasmlar asosida quyidagi savollarga ja- vob yozing va ularni...
1 - у скількох молекулах оксиду азоту NO міститься така сама кількість атомів, як у...
2 - д 5 Розглянь зображення. Дай відповіді на запитання. Сальмонела Ботулінова паличка...
1 - Прочитайте текст, выпишите глаголы, объясните образования, разберите по составу....
2 - Произведение Капитанская дочка заполнить таблицу...
2 - НАПИСАТЬ ЭССЕ НА ТЕМУ Many people agree that teenagers don t get enough exercise....
3 - вас . Придумать текст из 6 СПП(Сложно Подчиненных предложений) и 2 простых предложений...
1 - При каком значении p график y+px=0 пройдёт через точку пересечения прямых y=2/7x-21...
3 - Что из перечисленного является инструментом для автоматизации действий веб-браузера?...
2 - Разобрать морфологический разбор деепричастие слова: 1)Оленёнок, ОЩИПЫВАЯ листочки...
1
Объяснение:
___________________________