Алгебра, 8 класс Неполные квадратные уравнения
Решите с подробным решением
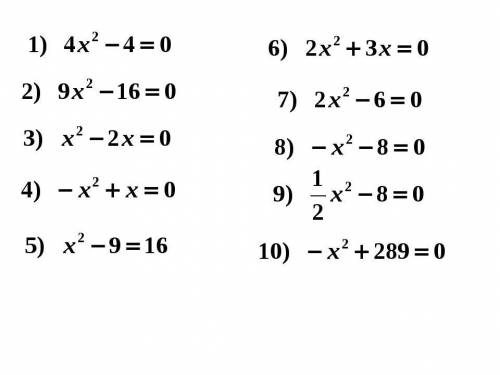
Другие вопросы по теме Алгебра
Популярные вопросы
- Определить температуру горения дизельного топлива в идеальной тепловой...
3 - Як склалися відносини між колоністами європейцями та місцевими жителями?...
2 - Охарактерезуй важнейшие изменения в политической и социально-економической...
3 - Дан рекурсивный алгоритм: procedure F(n: integer); begin writeln( *...
2 - Составить кроссворд о лапте с во и ответами ...
1 - «Объявляется во всенародное известие. Понеже в Сибирской губернии и...
3 - Укажите коэффициент перед формулой вещества X в схеме превращения,расставьте...
3 - 4. Заимствование и использование человеком в своих целях изобретений...
2 - Подробно описать героев из стих. Лермонтова русалк а...
2 - 1. Вступительное слово учителя Ребята, недавно в автобусе я увидела...
2
x^2 = 9
Для решения этого уравнения, мы должны найти значение переменной x, которое удовлетворяет данному уравнению.
Шаг 1: Возведение в квадрат
Чтобы избавиться от квадрата на левой стороне уравнения, возведем обе стороны уравнения в квадрат:
(x^2)^2 = (9)^2
x^4 = 81
Теперь наше уравнение имеет вид: x^4 = 81
Шаг 2: Извлечение корня
Чтобы найти значение x, мы извлечем корень четвертой степени из обеих сторон уравнения:
(sqrt(x^4)) = (sqrt(81))
Так как корень степени 4 "снимает" степень 4, оставляя только значение x:
x = sqrt(81)
Шаг 3: Вычисление значения корня
Мы должны найти квадратный корень из 81. Извлечение квадратного корня означает нахождение числа, которое при умножении на себя дает 81:
x = sqrt(81)
x = 9
Ответ: x = 9
Таким образом, значение переменной x, удовлетворяющее неполному квадратному уравнению x^2 = 9, равно 9.