Алгебра. №1
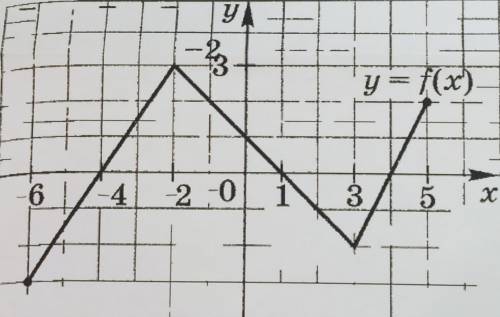
Определите по графику (см.фото) функции y=f(x) его промежутки:
а) монотонности;
б) знакопостоянства.

№2
Докажите, что функция:
а) f(x) = -x²+8x убывает на промежутке x=[4; +∞);
б) g(x) = -2/x-3 + 4 возрастает на промежутке x=(3; +∞).

№3
Определите промежутки знакопостоянства функции:
а) f(x) = x/5 + 1;
б) f(x) = (x-4)(x+3)/(x-2)(x+1)

P.S опишите решения максимально подробно.

№1
а) Для определения промежутков монотонности функции, нам необходимо проанализировать наклон графика. Если график функции возрастает, то она монотонно возрастает; если график функции убывает, то она монотонно убывает.

Из графика видно, что функция сначала возрастает (на промежутке от -∞ до точки минимума), затем убывает (от точки минимума до точки максимума), и снова возрастает (от точки максимума до +∞).

Таким образом, промежутки монотонности функции y=f(x) следующие:
- От -∞ до точки минимума,
- От точки максимума до +∞.

б) Для определения промежутков знакопостоянства функции, необходимо проанализировать, в каких интервалах функция принимает положительное и отрицательное значение.

Из графика видно, что функция положительна на промежутке от точки минимума до точки максимума, и отрицательна на промежутках от -∞ до точки минимума, а также от точки максимума до +∞.

Таким образом, промежутки знакопостоянства функции y=f(x) следующие:
- От -∞ до точки минимума,
- От точки минимума до точки максимума,
- От точки максимума до +∞.

№2
а) Для доказательства убывания функции на промежутке x=[4; +∞), необходимо показать, что при увеличении значения x функция f(x) уменьшается.

Используя квадратное уравнение f(x) = -x²+8x, найдем его производную:
f'(x) = -2x + 8.

Теперь найдем точку, в которой производная равна нулю и проверим ее знаки:
-2x + 8 = 0,
2x = 8,
x = 4.

Из предыдущего анализа графика, мы видим, что функция, сначала возрастает, а затем убывает. То есть, промежуток, начиная с x=4 и больше, будет промежутком убывания функции.

б) Для доказательства возрастания функции на промежутке x=(3; +∞), необходимо показать, что при увеличении значения x функция g(x) увеличивается.

g(x) = -2/x-3 + 4.
Получим общий знаменатель: g(x) = (-2 + 4(x-3))/(x-3).

Далее, найдем производную: g'(x) = (4)/(x-3)².

Найдем точку, в которой производная равна нулю и проверим ее знаки:
(4)/(x-3)² = 0,
4 = 0,
Получили невозможное равенство, значит, у функции g(x) нет точек, в которых производная равна нулю. Это означает, что функция возрастает на всем промежутке x=(3; +∞).

№3
а) Для определения промежутков знакопостоянства функции f(x) = x/5 + 1, необходимо проанализировать, в каких интервалах функция принимает положительное и отрицательное значение.

Функция линейная и увеличивается при увеличении значения x. Значит, она положительна на всем промежутке.

Таким образом, промежуток знакопостоянства функции f(x) = x/5 + 1 следующий:
- На всем множестве действительных чисел функция положительна.

б) Для определения промежутков знакопостоянства функции f(x) = (x-4)(x+3)/(x-2)(x+1), необходимо проанализировать, в каких интервалах функция принимает положительное и отрицательное значение.

Для этого, найдем нули в функции, то есть значения x, при которых функция равна нулю:
(x-4)(x+3) = 0,
x-4 = 0 или x+3 = 0,
x = 4 или x = -3.

Затем построим таблицу знаков:
x <-∞ | -3 | 4 | +∞
f(x) | + | 0 | + | +

Из таблицы знаков видно, что функция f(x) положительна на промежутках (-∞, -3) и (4, +∞) и отрицательна на промежутке (-3, 4).

Таким образом, промежутки знакопостоянства функции f(x) = (x-4)(x+3)/(x-2)(x+1) следующие:
- На промежутке (-∞, -3) и (4, +∞) функция положительна,
- На промежутке (-3, 4) функция отрицательна.