Ab(a+b)≤a³+b³ если a≥0 b≥0
Другие вопросы по теме Алгебра
Популярные вопросы
- Спирты Написать структурные формулы спиртов 3,4-диетилпент-1-ол;...
1 - решитьy={a×sin ax-1/(ax^2+1)Низ:(ax-1)^3 >...
3 - У помірному поясі вводиться близько декілька десятків видів земноводних...
3 - Выразите переменную очерез переменную ав выражении 2а + 3b =...
2 - Діеприслівниковий зворот це...
3 - К фундаментальным идеям Библии относят (укажите все правильные...
1 - У меня полтора часа на ответ 50-150 словРусский мат: происхождение,...
1 - Розв яжіть рівняння sin2x=0 на проміжку [0;2π]...
1 - Написать уравнения диссоциации следующих веществ: Ba(NO3)2, LiOH,...
1 - Опишите внешность людей, как показано в образце (example)....
1
Объяснение:
ab(a+b)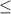 (a+b)(
(a+b)(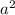 -ab+
-ab+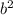 )
)
(a+b)(ab-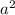 +ab-
+ab-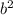 )
)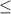 0
0
-(a+b)(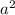 -2ab+
-2ab+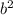 )
)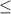 0
0
(a+b)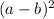
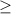 0
0
Первый множитель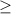 0 (по условию a≥0 b≥0), второй тоже
0 (по условию a≥0 b≥0), второй тоже 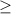 0 (квадрат). Значит и их произведение
0 (квадрат). Значит и их произведение 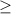 0. ЧТД.
0. ЧТД.