А)Упростите выражение: 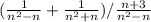 б)Найдите значение полученного выражения при n = -1.
б)Найдите значение полученного выражения при n = -1.
Другие вопросы по теме Алгебра
Популярные вопросы
- Будь ласка до ть ві хто до буду дуже вдячна вам все на фото заздалегідь...
2 - Выбери формулу вещества, с которого можно осуществить превращение:...
2 - Доповніть кожне з поданих реченьтак, щоб при цьому утворилося складносурядне...
1 - Part I Из четырех вариантов выберите единственный правильный. 1....
1 - Два автомобиля двигались с одинаковой скоростью и проехали 585км....
3 - Сколько монобромпроизводных может образоваться при бромировании...
3 - При якій умові електрон що повязаний з атомом, не випромінює енергію?...
3 - Определить степени окисления атомов в веществах: СН4, NH3, N2O5,...
3 - Рассмотрите рисунок и запишите пары конгруэнтных отрезков...
2 - Графічно розв яжи систему рівнянь: {y=x√y=x...
2
а) Для упрощения данного выражения, мы можем сначала найти общий знаменатель для обеих дробей в числителе. Знаменатели у нас: (n^2 - n) и (n^2 + n). Для того, чтобы найти общий знаменатель, мы должны перемножить эти два знаменателя.
(n^2 - n) * (n^2 + n) = n^4 - n^2 + n^3 - n^2 = n^4 + n^3 - 2n^2
Получаем: ((1 / (n^2 - n)) + (1 / (n^2 + n))) / ((n + 3) / (n^2 - n)) = ((1 / (n^2 - n)) + (1 / (n^2 + n))) * ((n^2 - n) / (n + 3)) = (1 + (n^2 - n) / (n^2 + n)(n + 3))
=(1 + (n^2 - n) / (n(n + 1))(n + 3))
б) Теперь мы должны найти значение полученного выражения при n = -1. Заменяем n на -1:
(1 + ((-1)^2 - (-1)) / (-1( -1 + 1))(-1 + 3)) = (1 + (1 - (-1)) / (-1 * 0)(2)) = (1 + 2 / (-1 * 0)(2))
Поскольку у нас в знаменателе 0, то это неопределенное значение, и у нас нет определенного ответа.