1. Алгебра
  2. А)решите уравнение 11*4^x

А)решите уравнение 11*4^x - 3*2^x+2 + 1 = 0. б) укажите корни этого уравнения, принадлежащие отрезку [-5; -3].

Hdjshddh Hdjshddh    2   18.03.2019 16:00    1

Ответы
vgirenkov vgirenkov  07.06.2020 03:36

11*4^x - 3*2^{x+2} + 1 = 0; \\ 11*4^x - 3*2^x *2^2 + 1 = 0;\\ 11*4^x - 3*2^x *4 + 1 = 0;\\ 11*4^x - 12*2^x + 1 = 0;\\ 11*4^x - 11*2^x -2^x + 1 = 0;\\ 11*2^x(2^x -1)-(2^x - 1) = 0;\\ (11*2^x-1)(2^x-1)=0; 1) 11*2^x-1=0; 11*2^x=1; 2^x=\frac{1}{11}; x_1=log_2 \frac{1}{11}; 2) 2^x-1=0; 2^x=1; 2^x=2^0; x_2=0

0 не принадлежит отрезку [-5;-3]. (очевидно)

так как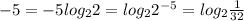 -5=-5 log_2 2=log_2 2^{-5}=log_2 \frac{1}{32}

-3=-3 log_2 2=log_2 2^{-3}=log_2 \frac{1}{8}

то первый корень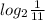 log_2 \frac{1}{11} указанному отрезку принадлежит

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
aisha834 aisha834  24.04.2019 13:21
Найдите все значения числа а при которых (a+3)x2+(a+2) имеет два корня ​...
ЯковПервый ЯковПервый  24.04.2019 13:27
Исключите аррациональность в знаменателе 1/√3 - √2​...
Kell500 Kell500  24.04.2019 13:29
Решите примеры с объяснением: 1)12a²b³+3a³b²+16b²-a² 2)49c²-14c+1-21ac+3a 3)ax²+ay²+x⁴+2x²y²+y⁴ 4)27c³-d³+9c²+3cd+d² 5)b³-2b²-2b+1...
AnyaManankina AnyaManankina  20.05.2019 15:34
Решите неравенства 1) -2x²+x+1≤0; 2) 4x²-4x+1≤0...
Dfh32 Dfh32  20.05.2019 15:35
Решите сейчас! внутри треугольника abc взята точка d, такая, что abd=acd=45 градусов. докажите, что отрезки ad и dc перпендикулярны и равны, если угол bac равен 45 градусов....
T0nystark T0nystark  20.05.2019 15:35
Найти значение выражения 23 в степени -4 / 23 в степени -6 объясните как получилось...
2001snk 2001snk  20.05.2019 17:00
Решить ленейное кравнение только так чтобы было понятно (x+8y=-6, (5x-2y=12...
Найк2006 Найк2006  20.05.2019 15:36
Как делить целые числа например: 8,4: 2,4=? объясните каждую мелочь....
aser101q aser101q  20.05.2019 17:00
Игральный кубик бросают дважды. найдите вероятность того, что произведение выпавших очков равно 12...
мария2386 мария2386  20.05.2019 17:00
Флакон шампуня стоит 160 рублей. какое наибольшее число флаконов можно купить на 1000 рублей во время распродажи, когда скидка составляет 25%?...

Популярные вопросы