(! a-это альфа,b-это бетта ) первое зад. : докажите тождество 1-tg a / 1+tg a = tg(45º-a) второе зад. : вычислите 1)зная,что tg a = 3 и tg (a-b) =1,вычислите tg b. 2)зная,что tg a =1/4 и tg (a-b) =2,вычислите tg b. третье зад. : известно,что cos a = 3/5, 0< a < 3п/2 вычислите: а) tg ( a+п/3) б) tg (a-5п/4)

Ответы

gustzhatetskiy 27.05.2020 10:50

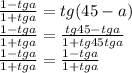
1) $\frac{1-tga}{1+tga}= tg(45-a)\\ \frac{1-tga}{1+tga}= \frac{tg45-tga}{1+tg45tga}\\ \frac{1-tga}{1+tga}= \frac{1-tga}{1+tga}\\$

верно

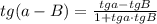
2) $tg(a-B) = \frac{tga-tgB}{1+tga\cdot tgB}$

подставляем tga =3

$tg(a-B) = \frac{tga-tgB}{1+tga\cdot tgB}=1\\ \frac{tga-tgB}{1+tga\cdot tgB}=1\\ \frac{3-tgB}{1+3\cdot tgB}=1\\ 3-tgB=1+3tgB\\ 4tgB=2\\ tgB = \frac{1}{2}$

аналогично следующая

$tg(a-B) = \frac{tga-tgB}{1+tga\cdot tgB}=2\\ \frac{tga-tgB}{1+tga\cdot tgB}=2\\ \frac{\frac{1}{4}-tgB}{1+\frac{1}{4}\cdot tgB}=2\\ \frac{1}{4}-tgB=2+\frac{1}{2}tgB\\ \frac{3}{2}tgB=-\frac{7}{4}\\ tgB = -\frac{7}{6}$

3) Поскольку косинус положительный, то угол принадлежит первой четверти. Значит все остальные функции тоже положительные.

Найдем синус:

$sina=\sqrt{1-cos^{2}a}= \sqrt{1-\frac{9}{25}}= \frac{4}{5}$

Разложим формулы тангенса и подставим значения синуса и косинуса:

$tg(a+\frac{\pi}{3}) = \frac{tga+tg\frac{\pi}{3}}{1-tgatg\frac{\pi}{3}}= \frac{tga+\sqrt{3}}{1-\sqrt{3}tga} = \frac{\frac{sina}{cosa}+\sqrt{3}}{1-\sqrt{3}\frac{sina}{cosa}}=\frac{\frac{4}{5}\cdot \frac{5}{3}+\sqrt{3}}{1-\sqrt{3} \cdot \frac{4}{5} \cdot \frac{5}{3}} = \frac{\frac{4}{3}+\sqrt{3}}{1-\frac{4}{3}\sqrt{3}}$