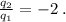А. (c^2 - 8)2 + 4(c^2 – 8) – 5 = 0;
В. (m2 + 6m – 1)^2 + 8(m2 + 6m – 1) = 9;
C. (2q - 1)^4 – 25(2q - 1)^2 + 144 = 0;
D. 4(х + 5)^4 =5(х + 5)^2 - 1.
Какое из данных уравнений имеет иррациональный
корень, меньше -3?
Какое уравнение имеет наименьший целый корень?
Два корня какого уравнения лежат на отрезке от 1,9 до
2.5?
У какого уравнения среди корней найдутся такие, что
Их отношение равно 2?
Другие вопросы по теме Алгебра
Популярные вопросы
- Сколько минут содержит в четверти, в одной трети, в одной шестидесятой...
3 - Девочка забыла вторую цифру в коде замка 8*5723 но помнила что все...
2 - Найдите наибольшее возможное значение x+y, если x,y — натуральные...
3 - 1. в аттракционе мертвая петля небольшие кабины соединены друг с...
3 - Вклассе 28 учащихся, 15 человек посещают кружок, 12 биологический,...
2 - Укажи побудительное предложение.1) как зовут этого мальчика? 2)...
3 - Подберите к словам однокоренные слова другой части речи: толщина,...
1 - Втреугольнике авс угол а=60градусов, ав=2см ас=3см найти сторону...
3 - Вкниге 888 страниц. сколько раз при нумерации страниц этой книги...
2 - Всостав процессора входят: а) озу б) принтер в) микроскопическая...
3
1) Какое из данных уравнений имеет иррациональный
корень, меньше -3? Это уравнение В . Корень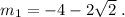
2) Какое уравнение имеет наименьший целый корень? Это уравнение D . Корень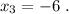
3) Два корня какого уравнения лежат на отрезке от 1,9 до 2,5 ? Нет таких уравнений .
4) У какого уравнения среди корней найдутся такие, что их соотношение равно 2? Нет такого уравнения. У уравнения С соотношение между 2 и 1 корнями равно (-2) ,