A,b- неотрицательные числа. Докажите неравенство
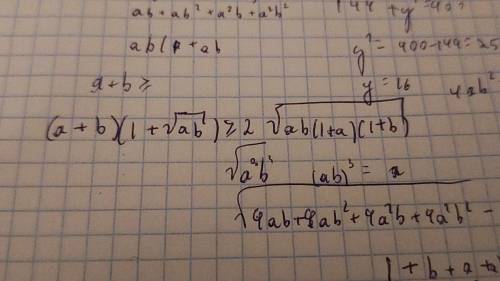
Другие вопросы по теме Алгебра
Популярные вопросы
- (154+246)-400 350:(785-435) 740*(1000:100):100 (856-234-621)*75...
3 - арман улучшил свой бизнес и в 2005 году получил чистую прибыль...
3 - Перечислите общие черты культуры России и Западной Европы XVIII...
3 - Как сказалась опричнина на положение привилигированных сословий...
2 - Петя съел 15 яблок сколько выйдет рюков если лайт будет срать...
3 - Решите уравнение: 3(4b-1)-2=12b+5 0 b - любое число корней нет...
3 - Турист проехал 100 км на автобусе и 45 км на поезде. Скорость...
3 - с решением 5=2:(1-3:(1+2:(1-1:(1+x...
2 - 1. |5x – 4| =10. 2. |2x – 6|+|x+2|+5= 0.3. |3x - 5| = x-1.4. |3x+2|...
2 - Напишите формулы оксидов,которые соответствуют гидроксидам Al(OH)3...
1
Раскроем слева скобки: (по нер-ву между ср. а и ср. г). Далее то же неравенство:
(по нер-ву между ср. а и ср. г). Далее то же неравенство: 