9 класс. f(x) = 3x^2 + 8x + 5
Задание 1.Найти меньшее значение функции.
Задание 2.Указать промежуток роста графика функции
Задание 3.Найдите значение аргументов,при которых функция принимает не отрицательных значений

1.  

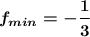
2.   Функция возрастает на промежутке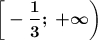  

3.   функция принимает не отрицательныe значения  при

Объяснение:

f(x) = 3x² +  8x + 5

1.   Найти меньшее значение функции.

График этой функции - парабола ветвями вверх.

Минимум функции достигается в вершине параболы.

Координата х₀ вершины по формуле

Тогда

2.  Указать промежуток роста графика функции

Функция возрастает на промежутке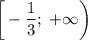  

3. Найдите значение аргументов, при которых функция принимает не отрицательные значения

3x² +  8x + 5 ≥ 0

Сначала найдем нули функции

Приведем квадратное уравнение и применим  теорему Виета

 - при этих значениях функция  f(x) = 0

И теперь, поскольку это парабола ветвями вверх,  неравенство  

3x² +  8x + 5 ≥ 0 выполняется при