9.10. а бұрышын а= a + 2пп (мұндағы п — бүтін сан және 0 < a.o < 2п) түрінде жазыңдар:
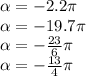
Популярные вопросы
- Дескрипторы: - определяет принадлежность достижений древних людей палеолита; -...
1 - Проверочный тест «чередующиеся гласные в корне», 5 класс 1. укажите слово с орфографической...
1 - 493. Есептеңдер: 11—1 1 11+ + + ... +100 100 100 100+31 1 1+3 2 2 23 38 рет15...
3 - Автомобіль проїхав за 30 хв 80 км ,за 40 хв - 60км . Визначити середню швидкісьть...
1 - напишите эссе на тему экстремальные виды отдыха , в эссе употребить предложения...
1 - Розв язати нерівність 3x 18...
3 - Вещество, которое обладает постоянным составом и постоянными физическими свойствами....
3 - Постройте профиль линии местности...
3 - обчисліть ступінь дисоціації якщо відомо що за температури 20° у воді розпалося...
2 - Подскажите как правильно выполнить это задание. Отдам за это ...
3
Для начала, давайте разберемся, что означают все обозначения в данной задаче:
- α - это значение угла в радианах.
- п - это обозначение для числа пи, которое примерно равно 3.14159.
- a - это переменная, значение которой необходимо определить. Значение a должно быть таким, чтобы предложенные равенства выполнялись.
Теперь давайте пошагово подставим значение a + 2пп в каждое из предложенных равенств и проверим их.
Равенство 1: α = -2.2π
Подставляем значение a + 2пп:
a + 2пп = -2.2π
Раскрываем скобки:
a + 6.28318 = -2.2π
Вычитаем 6.28318 из обеих частей уравнения:
a = -2.2π - 6.28318
Упрощаем выражение:
a = -8.48318π
Равенство 2: α = -19.7π
Подставляем значение a + 2пп:
a + 2пп = -19.7π
Раскрываем скобки:
a + 6.28318 = -19.7π
Вычитаем 6.28318 из обеих частей уравнения:
a = -19.7π - 6.28318
Упрощаем выражение:
a = -26.98318π
Равенство 3: α = -23/6π
Подставляем значение a + 2пп:
a + 2пп = -23/6π
Раскрываем скобки:
a + 6.28318 = -23/6π
Вычитаем 6.28318 из обеих частей уравнения:
a = -23/6π - 6.28318
Упрощаем выражение:
a = -26.98318/6π
Равенство 4: α = -13/4π
Подставляем значение a + 2пп:
a + 2пп = -13/4π
Раскрываем скобки:
a + 6.28318 = -13/4π
Вычитаем 6.28318 из обеих частей уравнения:
a = -13/4π - 6.28318
Упрощаем выражение:
a = -20.56718/4π
Таким образом, мы получили четыре значения переменной a, которые удовлетворяют данному равенству a = a + 2пп, а именно:
- a = -8.48318π
- a = -26.98318π
- a = -26.98318/6π
- a = -20.56718/4π
Надеюсь, данное объяснение было понятным для школьника. Если у вас возникли дополнительные вопросы, не стесняйтесь задавать их!