8.16 Найдите знаки корни уравнения если они существуют не решая уравнения

Другие вопросы по теме Алгебра
Популярные вопросы
- 1. По 1 главе выписать, как выглядели Настя и Митраша и как их называли. 2. ответить...
2 - При каком значении а пара чисел (-4; 2) является решением уравнения: 1) 3х + 5у...
2 - Реформация оставила в истории глубокий след, она изменила. Реформация вызвала...
1 - 3,4,6 задание сделайте . Заранее...
3 - Кут при вершині рівнобедреного трикутника дорівнює 60°. Тоді кути при основі дорівнюють...
3 - Якщо 1% числа становить 4,9, то все число...
1 - по графику сделать вывод грамотный. Как изменилась численность населения Украины...
2 - Оберіть правильне пропущене слово. Від самого початку Сулла розгорнув терор проти...
1 - Побудуйте пряму а і т. А, що не лежить на цій прямій. Проведіть пряму, що проходить...
3 - Якщо в рівнянні 5(х-3)= - 2(3+х) розкрити дужки й перенести доданки з однієї частини...
2
1)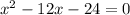
данное уравнение имеет два различных корня.
по теореме Виета:
Т.к. произведение корней отрицательно, то два корня разных знаков: меньший - отрицательный, больший - положительный.
2)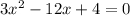
уравнение имеет два различных корня.
по теореме Виета:
Т.к. произведение корней положительно, то имеет два корня одного знака, а т.к. сумма корней положительна, то имеет два положительных корня.
3)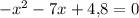
уравнение имеет два различных корня. По т. Виета:
Т.к. произведение корней отрицательно, то имеет два корня различных знаков: меньший - отрицательный, больший - положительный.
4)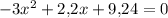
уравнение имеет два различных корня. По т. Виета:
Т.к. произведение корней отрицательно, то имеет два корня разных знаков: меньший - отрицательный, больший - положительный.