(7xy-3x²)+9x²-(6x²+2xy) , x-1⅘, y-2 1/19
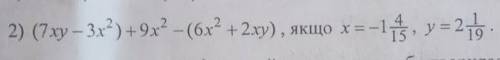
Популярные вопросы
- 1.известно, что оксиды азота в с.о.+3 и+5 являются кислотными. составьте...
1 - Разложить на множители (х+3)^2 - (х-3)^2...
1 - (укр)іть скласти власну конституцію україни на урок історії (рус) создать...
1 - Решить практическую работу по 6 класс,n°4. 15-20 ...
1 - 40 . составить таблицу по теме культура и повседневная жизнь народов россии...
3 - Используя рисунок, опишите цепочку превращения трех видов энергии. все...
1 - Напишите информационные листовки ко дню святого патрика на и...
3 - 1) определите массу, если образовавшийся при взаимодействии naoh и 200...
3 - Запишите множество значений х, при которых дробь х/6 будет правильной,...
3 - Вписанный угол abc опирается на дугу ac. найдите ∠ abc, если ⌣ac = 166...
2
(7xy-3x²)+9x²-(6x²+2xy)
Для начала, давайте посмотрим на выражение внутри скобок (7xy-3x²). Это часть, которую нужно сложить с остальными выражениями.
Теперь посмотрим на остальные выражения: 9x² и (6x²+2xy). Их необходимо вычесть.
Теперь приступим к пошаговому решению:
1. Начнем с выражения внутри скобок (7xy-3x²):
- У нас есть два монома: 7xy и -3x².
- Обратите внимание, что у них разные переменные и степени.
- Все переменные у нас разные (x, y), поэтому мы оставляем их как есть.
- Теперь посмотрим на степени. У первого монома у нас x имеет степень 1, а у второго x во второй степени.
- Чтобы сложить мономы, мы должны иметь одинаковую степень для каждой переменной.
- Для этого увеличим степень x в первом мономе до второй степени, получив 7x²y.
- Теперь мы можем сложить два монома: 7x²y - 3x².
2. Теперь посмотрим на остальные выражения: 9x² и (6x²+2xy):
- Мы должны вычесть (6x²+2xy) из 9x².
- Посмотрим на переменные: у нас есть x и y.
- У первого выражения x во второй степени, а у второго x во второй степени и y в первой степени.
- Это означает, что мы можем сложить одну переменную x в обоих выражениях и одну переменную y только во втором выражении.
- Посмотрим на степени: у нас x и y в первой степени в первом выражении, а x во второй степени и y в первой степени во втором выражении.
- Сложим переменные x: 9x² - 6x² = 3x².
- Пока у нас нет других переменных, которые мы можем сложить.
- Остается нам только y: 3x² - (6x²+2xy).
- Теперь мы можем вычесть мономы с переменной y: -2xy.
- Итак, окончательное выражение будет: 3x² - 6x² - 2xy.
Теперь мы можем объединить результаты по действиям со скобками и без них:
(7xy-3x²) + 9x² - (6x²+2xy) = 3x² - 6x² - 2xy + 9x²
Итак, итоговое выражение будет: 3x² - 6x² - 2xy + 9x².
Это и есть решение задачи.