7tg^2x+3tgx+2cos^2x-7cosx+1=0

Объяснение:

7tg^2 x + 3tg x + 2cos^2 x - 7cos x + 1 = 0

Можно применить универсальную тригонометрическую подстановку.

t = tg(x/2), тогда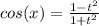 , 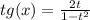. Подставляем:

Приводим к общему знаменателю (1-t^2)^2*(1+t^2)^2:

Избавляемся от дробей:

28t^2(1+2t^2+t^4) + 6(t-t^3)(1+2t^2+t^4) + 2(1-2t^2+t^4)(1-2t^2+t^4) -

- 7(1+t^2)(1-3t^2+3t^4-t^6) + (1-2t^2+t^4)(1+2t^2+t^4) = 0

Раскрываем скобки:

28t^2 + 56t^4 + 28t^6 + 6t - 6t^3 + 12t^3 - 12t^5 + 6t^5 - 6t^7 + 2 - 4t^2 + 2t^4 -

- 4t^2 + 8t^4 - 4t^6 + 2t^4 - 4t^6 + 2t^8 - 7 - 7t^2 + 21t^2 + 21t^4 - 21t^4 - 21t^6

+ 7t^6 + 7t^8 + 1 - 2t^2 + t^4 + 2t^2 - 4t^4 + 2t^6 + t^4 - 2t^6 + t^8 = 0

Приводим подобные:

t^8*(2+7+1) - 6t^7 + t^6*(28-4-4-21+7+2-2) - 6t^5 + t^4*(56+2+8+2+21-21+1-4+1)

+ 6t^3 + t^2*(28-4-4-7+21-2+2) + 6t + (2-7+1) = 0

10t^8 - 6t^7 + 6t^6 - 6t^5 + 66t^4 + 6t^3 + 34t^2 + 6t - 4 = 0

Делим все на 2

5t^8 - 3t^7 + 3t^6 - 3t^5 + 33t^4 + 3t^3 + 17t^2 + 3t - 2 = 0

Это уравнение имеет 2 иррациональных корня:

t1 = tg(x/2) ≈ -0,387

x/2 ≈ -arctg(0,387) + П*k

x1 ≈ -2arctg(0,387) + 2П*k, k ∈ Z

t2 = tg(x/2) ≈ 0,25

x/2 ≈ arctg(0,25) + П*k

x2 ≈ 2arctg(0,25) + 2П*k, k ∈ Z

В общем, у меня такое чувство, что в задании опечатка.

Слишком сложно получилось.

Ну, или это задание из математической спецшколы.