Алгебра: 75. Система рівнянь з параметром

(см. объяснение)Объяснение:Данную систему попробую решить чисто аналитически. Редко так деляю, поэтому надеюсь, что ничего не потеряю.Рассмотрим первую строку системы:Заметим, что при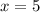 она теряет смысл.Действительно: , неверно.Выразим из рассматриваемого уравнения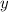 :Подставим полученную фразу во вторую строку системы:Упростим ее:ОДЗ для данной дроби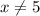 .Помня это, перейдем к более комфортной записи:При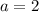 уравнение перестает быть квадратным. Это означает, что если мы получим x, не равный 5, то такое значение...

75.
Система рівнянь з параметром

75. Система рівнянь з параметром

Ответы

JoraUai0 11.08.2021 22:43

(см. объяснение)

Объяснение:

$\left\{\begin{array}{c}xy-5y-3=0\\x(y+2-a)-(3a+2)y-a+5=0\end{array}\right;$

Данную систему попробую решить чисто аналитически. Редко так деляю, поэтому надеюсь, что ничего не потеряю.

Рассмотрим первую строку системы:

xy-5y-3=0

Заметим, что при x=5 она теряет смысл.

Действительно: $5y-5y-3=0,\;\;-3=0$ , неверно.

Выразим из рассматриваемого уравнения :

$y=\dfrac{3}{x-5}$

Подставим полученную фразу во вторую строку системы:

$x\left(\dfrac{3}{x-5}+2-a\right)-(3a+2)\times\dfrac{3}{x-5}-a+5=0$

Упростим ее:

$\dfrac{(2-a)x^2+2x(2a-1)-4a-31}{x-5}=0$

ОДЗ для данной дроби $x\ne 5$ .

Помня это, перейдем к более комфортной записи:

(2-a)x^2+2x(2a-1)-4a-31=0

При a=2 уравнение перестает быть квадратным. Это означает, что если мы получим x, не равный 5, то такое значение параметра нужно взять в ответ.

$(2-2)x^2+2x(2\times2-1)-4a-31=0\\\\x=\dfrac{13}{2}$

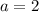Значит a=2 является фрагментом ответа.

При найденном вычислим :

$y=\dfrac{3}{\dfrac{13}{2}-5}\\\\y=2$

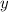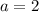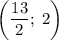Итого при a=2 система имеет единственное решение $\left(\dfrac{13}{2};\;2\right)$ .

При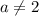 $a\ne2$ имеем параболу. Чтобы квадратное уравнение имело один единственный корень, нужно, чтобы его дискриминант был равен 0 (естественно, важно, чтобы тогда корень не был равен 5). В нашем случае еще допустимо, чтобы уравнение имело два корня, один из которых равен 5, так как по ОДЗ он не подойдет и в итоге из двух останется один.

Рассчитаем дискриминант, деленный на четыре (для более простого счета; можно считать обычный):

$\dfrac{D}{4}=(2a-1)^2+(2-a)(4a-31)=-27a+63$

Приравняем его к нулю:

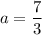$-27a+63=0\\\\a=\dfrac{7}{3}$

При $a=\dfrac{7}{3}$ исходная система уравнений имеет единственное решение 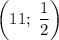$\left(11;\;\dfrac{1}{2}\right)$ . Берем его в ответ.

Подставим теперь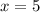 x=5 в наше уравнение:

$(2-a)\times5^2+2\times5\times(2a-1)-4a-31=0\\a=1$

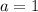При a=1 исходная система уравнений имеет единственное решение $\left(-7;\;-\dfrac{1}{4}\right)$ . Такое значение параметра подходит.

Итого:

При

система имеет единственное решение $\left(\dfrac{13}{2};\;2\right)$ При $a=\dfrac{7}{3}$ исходная система уравнений имеет единственное решение $\left(11;\;\dfrac{1}{2}\right)$ При a=1