723. Используя формулы полушария, вычислите: 1) 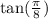
нужно выполнить
Другие вопросы по теме Алгебра
Популярные вопросы
- Перепишите вставляя нужные префиксы: по.вы.пере (a) (a) (a) (a) (a) (a)...
3 - Сколько одинаковых звуков в словах ива и вилка?...
1 - Мопед массой 100 кг разогнался из состояния покоя так, что его кинетическая энергия...
3 - От какого слова произошло слово пылеводонепроницаемые(часы) образец: одевшись-одеться...
3 - В300г воды растворили 30г сахара. массавая доля сахара в полученном растворе: 9%...
2 - Составить предложение со словами - сұлу, ана, ұстаз, шаһар....
1 - 3. расскажите,почему стала трудной жизнь васи дома после смерти матери? 5. как вы...
1 - Восемь школьников оставались в классе на перемене, и один из них разбил окно. на...
3 - Нужно! матрос галиота секрет предположил что капитан грей купил материал для парусов...
1 - Перевести из актива в пассив! 1. do they make bread in this factory? 2. will susan...
1
Из геометрии известно, что