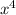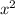6. Найти наибольшие и наименьшие значения функции y = − 2 на отрезке [-2;2]

Наибольшее значение функции равно 8, наименьшее -1.

Объяснение:

y =  х⁴ - 2х²

Найдём производную заданной функции:

y' = (х⁴ - 2х² )' = 4x³ - 4х

Найдём стационарные точки:

y'(0) = 0; ⟺ 4x³ - 4х  = 0; ⟺ 4х(х - 1)=0; ⟺ x₁ = 0; х₂ = 1.

Интервалу  [-2;2] принадлежат обе стационарные точки.

Найдём значение функции в критических точках и в концах отрезка:

y(0) = 0⁴ - 2 · 0² = 0

y(1) = 1⁴ - 2 · 1² = - 1

y(-2) = (-2)⁴ - 2 · (-2)² = 8

y(2) = 2⁴ - 2 · 2² = 8

Наибольшее значение функции равно 8, наименьшее -1.