1. Алгебра
  2. 6. Если ребро куба увеличить

6. Если ребро куба увеличить в 5 раз, то как изменится объём куба и площадь его сновани? ( оно прост не поместилось


6. Если ребро куба увеличить в 5 раз, то как изменится объём куба и площадь его сновани? ( оно прост

aliksondrrr3 aliksondrrr3    3   24.10.2021 23:41    56

Ответы
aevseeva03 aevseeva03  01.12.2021 02:31

1)\ \ P=3ab^3+(2ab^3+6a^2b)+(2a^2b+5a)=5ab^3+8a^2b+5a\\\\stepen\flat \ \ n=4\\\\2)\ \ 2az^2-3a^2z+2z^2-3az-a-1=2z^2(a+1)-3az(a+1)-(a+1)=\\\\=(a+1)(2z^2-3az-1)\\\\3)\ \ a=625\, 000\, 000=6,25\cdot 10^8\ \ \ ,\ \ \ b=0,000\, 003=3\cdot 10^{-6}\\\\ab=6,25\cdot 3\cdot 10^8\cdot 10^{-6}=18,75\cdot 10^2=1,875\cdot 10^3=1875

4)\ \ \displaystyle \Big(\frac{1}{4}\Big)^{-2}-\Big(-\frac{3}{8}\Big)^0+\Big(\frac{2}{3}\Big)^3:\frac{7}{9}=4^2-1+\frac{4}{9}\cdot \frac{9}{7}=16-1+\frac{4}{7}=\\\\\\=15+\frac{6}{7}=\frac{111}{7}=15\frac{6}{7}

5)  Пусть ребро куба равно  а .

Тогда его объём равен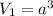   V_1=a^3  , площадь основания равна  S_1=a^2  .

Теперь ребро стало равно  5.

И объём куба с таким ребром равен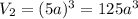   V_2=(5a)^3=125a^3   , а площадь  

основания равна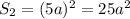    S_2=(5a)^2=25a^2 .

\dfrac{V_2}{V_1}=\dfrac{125a^3}{a^3}=125\ \ ,\ \ \ \dfrac{S_2}{S_1}=\dfrac{25a^2}{a^2}=25

Объём увеличился в 125=5³ раз , а площадь увеличилась в 25=5² раз .

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
namdokp09srw namdokp09srw  06.12.2021 23:09
Имеются два сплава свинца и меди. Первый сплав содержит 26 кг свинца и 24 кг меди, а второй - 24 кг свинца и 16 кг меди. На сколько процентов содержание свинца в первом...
tatyana101035 tatyana101035  06.12.2021 23:09
4. Решите систему уравнений графическим : {x+y=4;\\ 2x-y=2...
Ivanlabur Ivanlabur  06.12.2021 23:05
Решите уравнение и укажите корни этого уравнения, принадлежащие интервалу...
LerkaKsuphaMey LerkaKsuphaMey  06.12.2021 23:04
4. Решите систему уравнений графическим : {x+y=4;\\ 2x-y=2...
esmirakagraman esmirakagraman  23.04.2020 14:20
X 1,8 решите неравенства​...
trofimovakarina1 trofimovakarina1  23.04.2020 14:18
ХЕЛП, очень задания по алгебре...
megasashabori megasashabori  23.04.2020 14:18
решить. Решите в тетради под буквами а и б в каждом номере. Вынесите общий множитель за скобки в 4 номере нужно с начало перевести к общему знаменателю...
yanakuznetsova9 yanakuznetsova9  23.04.2020 14:20
решить систему уравнений методом подстановки...
driveSas driveSas  25.11.2021 21:09
7 Луч ОС лежит между сторонами угла АОВ=120º. Найдите LAOC и L ВОС, если LAOC :L BOC =3:5....
ulzhalgasamangEldy ulzhalgasamangEldy  25.11.2021 21:10
1. Розв яжіть рівняння: x(x - 2) 1) х*x + 4 = 0;...

Популярные вопросы