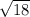6.а) При каких x значениях функция y =f(x)=-2x^2+2х -3 больше, чем соответствующие значения функции y=g(x)=-х-1?
б) При каких x значениях график функции y =f(x)=х/3 находится ниже графика функции y =g(x) =6/х?
Другие вопросы по теме Алгебра
Популярные вопросы
- Постройте гармонические оборо ы в си бемоль минор !...
2 - Приклади пароутворення випаровування та конденсації...
1 - Восьмая глава евгения онегина. онегин в петербурге, автор о герое...
2 - Какую связь имеет хлорид калия? примеры веществ с ионной связью....
1 - Складіть твір-роздум на тему: тільки любов до рідної землі, батьківської...
1 - 7) when they arrive) at the cinema, the film (begin) already. 8) we (not/dance)...
1 - 100 за правильний ответ.: визначити найвидатніші винаходи середньовіччя...
3 - Перестройте данные предложения в предложения с косвенной речью и запишите...
1 - На сколько кг 1 кубический метр массы свинца больше чем 1 кубический метр...
3 - Плиты для садовых дорожек в упаковках по 3 штуки. сколько упаковок плит....
3
Объяснение:
a) По условию составляем неравенство
-2x^2 + 2x -3 > -x -1
-2x^2 + 3x -2 > 0
2x^2 - 3x + 2 < 0
x^2 - 1.5x + 1 < 0
(x^2 - 0.75)^2 + 1 < 0 - не может быть ни при каких x, потому что значение выражения (x^2 - 0.75)^2 + 1 всегда положительно, значит, f(x) не будет больше g(x) ни при каких значениях x.
б) График функции y = f(x) находится ниже графика функции y =g(x), значит, выполняется неравенство f(x) < g(x)
x/3 < 6/x
x/3 - 6/x < 0
(x^2 - 18)/3x < 0
1.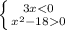 3x < 0 ⇒ x<0 ⇒ x < -
3x < 0 ⇒ x<0 ⇒ x < -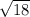
(x +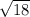 )(x -
)(x - 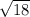 ) > 0 ⇒ x < -
) > 0 ⇒ x < -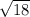 или x>
или x>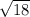
2.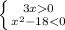 3x > 0 ⇒ x>0
3x > 0 ⇒ x>0
(x +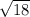 )(x -
)(x - 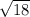 ) < 0 ⇒ x <
) < 0 ⇒ x < 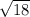 и x>-
и x>-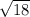 ⇒ 0<x <
⇒ 0<x < 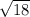
x < -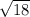 и 0<x <
и 0<x <