5^((x)^2-3x-2)/(6-x) больше или равно 0.2
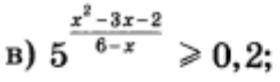
Другие вопросы по теме Алгебра
Популярные вопросы
- 1) выражение: cos альфа умножить tg альфа минус sin альфа, 2)найти...
2 - Электрон влетает в магнитное поле перпендикулярно силовым линиям...
3 - Надо.. при нагревании некоторого металла от 0 до 500° его плотность...
3 - Сейчас произведение возрастов чапы и паши равно 2 в степени 3 *...
3 - Придумать 5 сложных по за 7 класс...
3 - .(Определить э. д.с индукции возникающую в контуре проводника если...
2 - .(Магазин продал за 3 дня 1240.8кг. в 1 день продали 543,во 2 в...
1 - Удвух мышей-полевок родилось 15 мышат. сколько детенышей родилось...
2 - Найдите основание вс равнобедренного треугольника авс, если его...
3 - Решить систему уравнений: 2 в степени x = siny 2 в степени -x =...
3
Объяснение:
Показательная функция. Основание больше 1. Для степеня сохраняется знак неравенства
x =2 , x<6
Объяснение: