5. Розв'язати рівняння: 2х^2006 + 3x^2008 + 4x^2010 + 5х^2012 + 6х^2014 + 7x^2016 + 8x^2018 + 9х^2020 = 44х

Ответы

Бацио 19.01.2022 01:16

$2x^{2006}+3x^{2008} + 4x^{2010} + 5x^{2012} + 6x^{2014} + 7x^{2016} + 8x^{2018} + 9x^{2020} = 44x$

Заметим, что при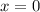 x=0 левая и правая часть уравнения обращается в 0. Значит, число 0 является корнем этого уравнения.

$\boxed{x_1=0}$

Предположим, что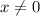 $x\neq 0$ . Тогда, мы можем разделить обе части равенства на . Получим:

$2x^{2005}+3x^{2007} + 4x^{2009} + 5x^{2011} + 6x^{2013} + 7x^{2015} + 8x^{2017} + 9x^{2019} = 44$

Рассмотрим левую часть.

Вспомним, что функция вида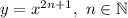 $y=x^{2n+1},\ n\in\mathbb{N}$ является возрастающей на всей области определения, то есть на множестве действительных чисел. Тогда и функция 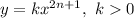$y=kx^{2n+1},\ k0$ является возрастающей. Сумма возрастающих функций также является возрастающей.

Применительно к данному уравнению можно записать: функции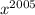 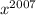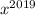$x^{2005}$ , $x^{2007}$ , ..., $x^{2019}$ возрастают, тогда и функции 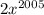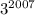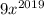$2x^{2005}$ , $3^{2007}$ , ..., $9x^{2019}$ также возрастают, а значит возрастает и их сумма.

Таким образом, функция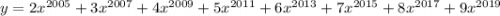 $y=2x^{2005}+3x^{2007} + 4x^{2009} + 5x^{2011} + 6x^{2013} + 7x^{2015} + 8x^{2017} + 9x^{2019}$ возрастает. Это означает, что каждое свое значение она принимает только в одной точке.

Следовательно, уравнение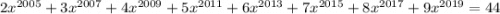 $2x^{2005}+3x^{2007} + 4x^{2009} + 5x^{2011} + 6x^{2013} + 7x^{2015} + 8x^{2017} + 9x^{2019} = 44$ может иметь не более одного решения.

Решение уравнения легко подбирается: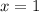 x=1 . Действительно, сумма коэффициентов в левой части уравнения равна 44: