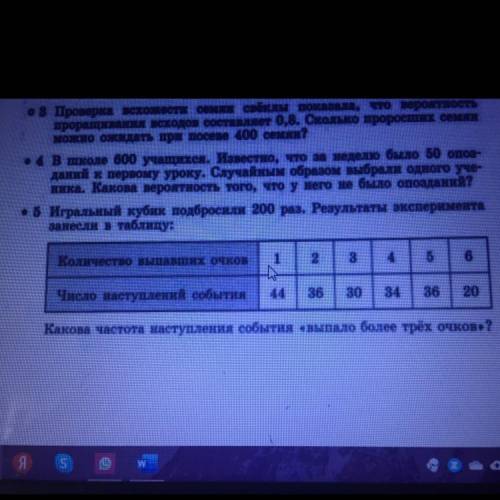
• 5 Игральный кубик подбросили 200 раз. Результаты эксперимента
занесли в таблицу:
Количество выпавших очков
1
2
3
5
6
Число наступлений события
36
30
34
36
20
Какова частота наступления события выпало более трёх очков?
Ооооочень решить мне сейчас 2 поставят
Другие вопросы по теме Алгебра
Популярные вопросы
- Предприятие изготовил о за квартал 700 насосов 60% имели высшую катигорию...
1 - Алгебра, 8 Класс Катер км по течению реки и 4 км по озеру, затратив...
2 - Подскажите не могу решить...
3 - Решить квадратичную функцию и показать её на графике, найти её вершину,...
2 - Характеристика Алексея Иванова в рассказе «Возвращение»...
1 - Ия:2 Б. При делении ядер урана 235/92Uо свобождается энергия 200 МэВ,...
2 - И Я ДАМ 0. КАКОВА ПРОБЛЕМА РАССКАЗА А. ПРИСТАВКИНА ЗОЛОТАЯ РЫБКА ?КАКИЕ...
2 - На подарок , упакованный к коробку формы прямоугольного параллелепипеда...
3 - 1. Специфика физического воспитания заключается в...а. повышении адаптационных...
1 - Составить сравнительную таблицу «Роль Земских Соборов при Михаиле Федоровиче...
2
По таблице мы видим, что количество выпавших очков "1" составляет 36 раз, "2" - 30 раз, "3" - 34 раза, "4" - не указано, "5" - 36 раз, "6" - 20 раз.
В данной задаче нас интересует количество выпадений очков, большее трех, то есть определение суммы выпавших очков "4", "5" и "6".
Чтобы найти это количество, сначала нужно сложить сколько раз выпали каждое из этих чисел. Таким образом, мы получим:
4 + 5 + 6 = 15
Теперь мы можем найти частоту наступления события "выпало более трёх очков", разделив сумму выпавших очков "4", "5" и "6" на общее количество подбрасываний, которое равно 200 раз:
Частота = (15 / 200) * 100
Для умножения и деления в процентах наоборот выполняют операцию, то есть сначала делим сумму выпавших очков на общее количество подбрасываний, а затем умножаем полученный результат на 100.
Частота = 15 / 200 * 100
= 0.075 * 100
= 7.5
Таким образом, частота наступления события "выпало более трёх очков" равна 7.5%.