480. Даны функции 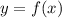 и
и 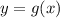 :
:
d)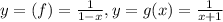
1) Запишите функции 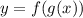 и
и 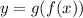
2) Верно ли уравнение 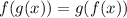
Другие вопросы по теме Алгебра
Популярные вопросы
- Составить РЕКЛАМУ о разведение кроликов...
2 - В первый день автомобиль проехал 2/7 . Во второй на 1/4 больше чем в первый.В третий...
3 - 6 В обувном магазине «Лапти» три отдела: мужской, женской идет-ской обуви. На диаграмме...
3 - ЛЮДИ СКОЛЬКО БУДЕТ 0,2 в обычном дробе...
2 - S ABC S A1B1C1S ABC=16смAB=6смA1 B1=3смS A1B1C1–?...
2 - 1.В урне находятся 10 шаров, 7 из которых белых. Найти вероят¬ность того, что из...
2 - Первидите это текст дословно...
2 - Прямая MN является секущей для прямых AB и CD(M принадлежит AB, N принадлежит CD)....
2 - Цитатна характеристика героїв Дон Кіхот...
1 - Как развивались события в ходе Крымской войны?...
1
f(x), где х - переменная.
f(1), 1 заменяет х, значит если вместо 1 будет g(x), то нам надо подставить вместо х функцию:
f(x) = 1/(1-x)
g(x) = 1/(x+1)
f(g(x)) = f(1/(x+1)) = (1 - 1/(x+1))^-1 = ((x+1-1)/(x+1))^-1 = (x/(x+1))^-1 = (x+1)/x
g(f(x)) = g(1/(1-x)) = (1/(1-x) + 1)^-1 = (-1/(x-1)+1)^-1, функции уже не равны.
(-1/(x-1)+1)^-1 = ((x-1-1)/(x-1))^-1 = (x-1)/(x-2)
1) f(g(x)) = (x+1)/x
g(f(x)) = (x-1)/(x-2)
2) неверно