453. Найдите наибольшее и наименьшее значения кубической функции 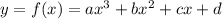 в интервале. a)
в интервале. a)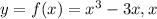 ∈[0;2]
∈[0;2]
b)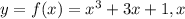 ∈[-3;3]
∈[-3;3]
Другие вопросы по теме Алгебра
Популярные вопросы
- Por favor, ayúdame a resolver los ejemplos, ¡te daré los puntos que solo están...
1 - 3х-5x - 2 - 0теңдеуінің дискримать та...
2 - АЛГЕБРА 11 КЛАСС С УРАВНЕНИЕМ. ОЧЕНЬ НУЖНО ХОРОШЕЕ РЕШЕНИЕ. 2x^3 + 7x^2 + 5x +...
2 - Read the story and complete ...
2 - Переведите на русский язык. Обозначьте корни и соединительные гласные в украинских...
2 - 2.Шығарма неге «Кенесары – Наурызбай» деп аталған? Сен- дер қандай атау ұсынар...
1 - 1. ТЕКСТ о коврах-это ... . а)художественный текст б)нехудожествиный текст 2....
3 - Вопрос по комедии Горе от ума почему Софья захотела отомстить Чацкому?...
3 - В результате диссимиляции образовалось 380 молекул АТФ? сколько из них образовалось...
2 - .Английский язык 2. Посмотри на картинку и прочти утверждения. Напиши «yes» или...
3
a)y(наиб)=2
y(наим)=-2
b)y(наим)=-29
y(наиб)=31
Объяснение:
a)
1)Находим производную функции :
f'(x)=3x^2-3
2) Приравниваем производную к 0 ( находим нули производной):
3x^2-3=0 --> x=1
x=-1
3) Промежутку принадлежит только точка x=1 , поэтому значения функции на концах и в точке 1:
f(0)=0
f(1)=-2-наим
f(2)=8-6=2-наиб
б)
1)Находим производную функции :
f'(x)=3x^2+3
2) Приравниваем производную к 0 ( находим нули производной):
3x^2+3=0 --> решений нет , значит наибольшее значение достигает правом конце отрезка [-3;3] , а наименьшее - в левом:
3) f(-3)=-27-3+1=-29
f(3)=27+3+1=31