41.5. решите уравнение f ' (x) = 0: f (x) = 5x^2-3x-1 / x-3;f (x)=2-5x^2/x^ 2+3x;f(x)=5x / x + 5-x; f(x)=x ^ 2 + 7x/x+3-2x/x + 3
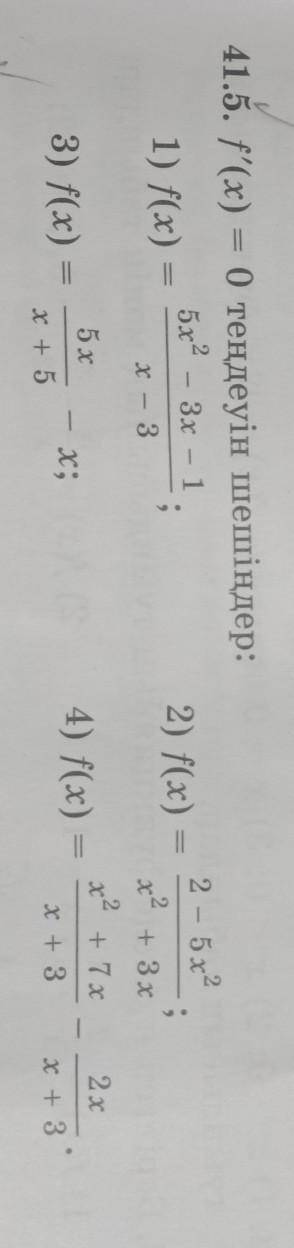
Другие вопросы по теме Алгебра
Популярные вопросы
- Окончание -ыть к какому спряжению относятся?...
3 - Скакой целью диалектные слова используются иногда в художественных...
3 - 1)каких животных робинзон крузо взял с коробля 2)возле жилища выросли...
1 - 1. в тексте поэмы гефест, щит для ахиллеса, называется художником....
3 - Какой вид связи используется в li2o? а) ионная б) ковалентная полярная...
3 - 1. а) sinx -1/2 б) cosx √2/2 в) tgx √32. sin (x- π/3) = √3/2 б) cos...
2 - 14. разрежьте фигуру по линиям на три одинаковые части. найдите периметр...
3 - Вкаком предложении не хватает двоеточия? они по дорожке ко входу...
3 - Выберите три верных ответа из шести и запишите цифры под которыми...
3 - 2сынып қазақ тілі 89 бет 55 жаттығу...
2
тебе как дообно фото прилать или напиать здеь
Объяснение:
a) Уравнение f'(x) = 0, где f(x) = (5x^2-3x-1) / (x-3):
Для начала найдем производную функции f(x):
f'(x) = [(2*5x - (5x^2-3x-1)*1)/(x-3)^2] = (10x - (5x^2 - 3x - 1)) / (x-3)^2
Уравнение f'(x) = 0:
(10x - (5x^2 - 3x - 1)) / (x-3)^2 = 0
10x - 5x^2 + 3x + 1 = 0
-5x^2 + 13x + 1 = 0
Для решения получившегося квадратного уравнения, можно воспользоваться формулой дискриминанта:
D = b^2 - 4ac, где a = -5, b = 13 и c = 1.
D = 13^2 - 4(-5)(1) = 169 + 20 = 189
Теперь найдем значения x, используя формулу:
x = (-b +/- √D) / 2a
x1 = (-13 + √189) / (-10)
x2 = (-13 - √189) / (-10)
x1 ≈ 2.08
x2 ≈ 0.12
Ответ: x ≈ 2.08 и x ≈ 0.12
b) Уравнение f'(x) = 0, где f(x) = (2 - 5x^2) / (x^2 + 3x):
Для начала найдем производную функции f(x):
f'(x) = [(2*(2x)*(x^2+3x) - (2-5x^2)*(2x+3))/(x^2+3x)^2] = (4x^3 + 6x^2 - (4x + 6)) / (x^2+3x)^2
Уравнение f'(x) = 0:
(4x^3 + 6x^2 - (4x + 6)) / (x^2+3x)^2 = 0
4x^3 + 6x^2 - 4x - 6 = 0
Попробуем найти рациональные корни этого уравнения. Так как 6 имеет мало делителей, начнем проверку с целых чисел:
Подставим x = 1 и x = -1:
4(1)^3 + 6(1)^2 - 4(1) - 6 = 0, НЕ ВЕРНО
4(-1)^3 + 6(-1)^2 - 4(-1) - 6 = 0, НЕ ВЕРНО
Пользуясь правилами деления многочленов, мы можем применить метод Ньютона или деление с остатком, чтобы найти другие корни. Однако данная задача является мнимой и ее корни не рациональные или раскладываемые на множители. Поэтому мы не можем найти точные значения корней уравнения.
Ответ: в данном случае мы не можем найти точные значения корней уравнения.
c) Уравнение f'(x) = 0, где f(x) = 5x / (x + 5 - x):
Для начала найдем производную функции f(x):
f'(x) = [((x + 5 - x)*(5) - (5x)*(1))/((x + 5 - x)^2)] = 0 / (x+5-x)^2 = 0
Уравнение f'(x) = 0:
0 = 0
Уравнение не зависит от значения x, поэтому любое значение x будет являться решением.
Ответ: x может быть любым действительным числом.
d) Уравнение f'(x) = 0, где f(x) = (x^2 + 7x) / (x+3) - (2x) / (x+3):
Для начала найдем производную функции f(x):
f'(x) = [((x+3)*(2x+7) - (x^2+7x)*1)/((x+3)^2)] = (2x^2 + 6x + 14 - (x^2 + 7x)) / (x+3)^2
f'(x) = (x^2 - 2x + 14) / (x+3)^2
Уравнение f'(x) = 0:
(x^2 - 2x + 14) / (x+3)^2 = 0
Поскольку делить на ноль нельзя, то знаменатель уравнения (x+3)^2 не может равняться нулю. Поэтому мы решаем только числитель (x^2 - 2x + 14) = 0.
Решаем получившееся квадратное уравнение:
D = (-2)^2 - 4(1)(14) = 4 - 56 = -52
D меньше нуля, следовательно, уравнение не имеет действительных корней.
Ответ: уравнение не имеет решений.