Алгебра: 4. Найдите область определения функции

4. Найдите область определения функции

Ответы

sysfzd 17.06.2021 14:41

$D(y)=(0;\ 2].$

Объяснение:

Для данной функции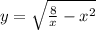 $y = \sqrt{\frac8x - x^2}$ есть два ограничения на область определения: первое, возникающее из-за квадратного корня и требующее, чтобы подкоренное выражение было неотрицательным, а также второе, возникающее из-за дроби, требующее, чтобы знаменатель дроби не был нулевым.

Получаем, что нужно решить неравенства:

$\frac8x-x^2 \geqslant 0,\\x\neq 0.$

Решим первое:

$\frac8x-x^2\geqslant 0;\\\frac{8-x^3}{x} \geqslant 0;\\\frac{2^3-x^3}{x} \geqslant0;\\\frac{(2-x)(2^2+2x+x^2)}{x} \geqslant 0.$

Разложив числитель на множители, мы можем решить неравенство методом интервалов. Выделим особые точки:

$2-x=0;\\x=2.$

$x\neq 0.$

$x^2+2x+4=0\\D=4-4\cdot4=4-16=-12.$

Корней нет. Точками для метода интервалов будут , .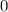

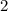Для всех точек левее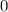 значение выражения будет отрицательным.

Для точек между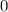 и 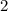значение выражения будет положительным.

Для точек правее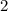 значение выражения будет отрицательным.

Получаем, что решением неравенства будет промежуток чисел от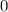 до 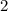. Поскольку неравенство нестрогое, промежуток должен включать свои границы, однако по причине наличия в системе неравенства 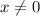$x\neq 0$ , исключающего из решения левую границу промежутка, итоговый промежуток будет иметь вид: $(0;\ 2].$