3sin²x-10 sinx-8=0
решить уравнение
Другие вопросы по теме Алгебра
Популярные вопросы
- Вычислить объем газа, который выделится при взаимодействии 240г магния, содержащего...
1 - Каков расход энергии за 40 с в автомобильной электрической лампочке, рассчитанной...
3 - Демократические изменения в современной россии. (начиная с конституции 1993)...
1 - Втреугольнике сде точка м лежит на стороне се,причем смд острый.докажите что де...
2 - Найди и запиши слова с не проверяемыми гласными и согласными в корне слова: качалка,...
3 - Около равнобокой трапеции, основания которой 7см и 25см, а боковые стороны 15см,...
1 - Скласти казку про пригоди гномів у лісі пару речень....
1 - 1) к прикладным программам относятся: 1 текстовые редакторы 2 графические редакторы...
2 - Сколько молекул содержится в 100 мл воды при 10с?...
2 - Нужно самой написать притчу небольшую предложений 5-10 поп укр-...
3
3sin²x-10 sinx-8=0
Пусть sinx=t, t<|1|, тогда
3t²-10t-8=0
D = (-10)²-4*3*(-8) = 100 + 96 = 196 = 14²
Вернёмся к замене:
sin x = -2/3
ответ: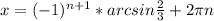 , n ∈ Z
, n ∈ Z