36.3.Найдите предел функции.
36.4.Найдите предел выражений.
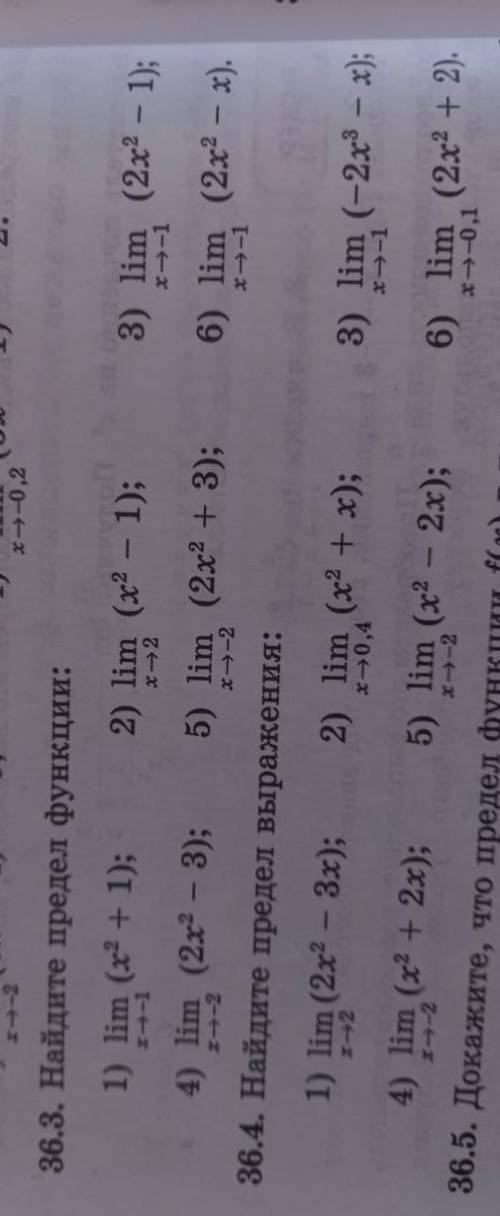
Другие вопросы по теме Алгебра
Популярные вопросы
- Заполните пропуски используя слова для справок ...
2 - Найдите sinα и tgα, если cosα=0,8...
2 - 2а) Среди чисел найдите взаимно обратные.Числа...
1 - только я буду очень благодарна...
3 - ТЕКСТ ЗАДАНИЯ Определите вид сказки по характерным признакам:Сюжет сказки...
1 - Я сосиску в тесте хочу, а меня тут французский заставляют делать, может...
2 - Этот исторический деятель в середине 10 века смог при арабской династииСаманидов...
3 - Написать обвинительную речь в адрес городничего. (Н.В. Гоголь Ревизор...
1 - Найдите значение выражения 81/a² при a=9...
3 - Напишіть формулу сполуки до складу якої входять 2 атоми Бору 3 атоми...
1
36.3. Найдите предел функции:
Для начала рассмотрим функцию представленную на графике.
Предел функции находится при приближении аргумента к некоторому числу. На графике видно, что приближая x к значению 2, значение функции стремится к -1.
Таким образом, предел функции при x→2 равен -1.
36.4. Найдите предел выражений:
а) При x→-2:
Из выражения видно, что в знаменателе присутствует (x + 2), что означает, что приближая x к -2, знаменатель будет равен 0. Поэтому здесь предел не существует.
б) Для функции g(x) при x→-2:
Аналогично предыдущему пункту, приближая x к -2, знаменатель становится равным 0. Однако в числителе также присутствует (x + 2), поэтому данное выражение можно упростить, сократив (x + 2) в числителе и знаменателе:
Lim (x-2)/(x+2) = Lim (x-2)/(x+2) = Lim 1 = 1
в) При x→0:
В числителе данного выражения присутствует x, в знаменателе - sin(x). Если приближать x к 0, то числитель стремится к 0, а знаменатель - к 0 (так как sin(x)→0 при x→0). Значит, мы имеем "0/0", что можно рассмотреть с использованием правила Лопиталя.
Применяя это правило к данному выражению, получим:
Lim sin(x)/x = Lim cos(x) = cos(0) = 1.
Описанные рассуждения позволяют нам найти пределы функции и выражений при приближении аргумента к определенным значениям. Если у вас появятся еще вопросы, не стесняйтесь задавать их. Я готов помочь вам разобраться еще более подробно.