1. Алгебра
  2. 35 f(x)=x^2-2x-3 найти: 1)

35 f(x)=x^2-2x-3 найти: 1) область значения функции 2) область убывания функции 3) множество решений неравенства f(x)< 0

kurbanbaevarseN kurbanbaevarseN    2   03.10.2019 20:30    4

Ответы
Алиса623 Алиса623  09.10.2020 15:19

f(x) = x^2 - 2x - 3

Найдём производную функции, для нахождения экстремума и промежутков убывания.

f'(x) = 2x - 2

1

Найдём минимум этой функции:

f'(x) = 0 \Rightarrow 2x - 2 = 0 \Rightarrow x = 1 \Rightarrow f(1) = -4 \text{ --- min}

Следовательно,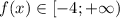 f(x) \in [-4; +\infty)

2

Функция убывает там, где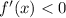 f'(x) < 0.

Т.е.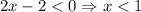 2x - 2 < 0 \Rightarrow x < 1.

Функция убывает на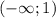 (-\infty; 1)

3

x^2 - 2x - 3 = (x - 3)(x + 1) < 0 \Rightarrow x \in (-1; 3)

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
bereza11 bereza11  08.04.2020 09:46
ответь на во по графику функции. 1 клеточка = 3 единицам. bildiite.PNG a) Сколько км будет преодолено через 24 минут? км. б) Через сколько минут будут (будет) преодолены (преодолён)...
vetoss2 vetoss2  08.04.2020 09:46
{2x + 3y = 7{5x - 4y = 6 решите уравнение методом подстановки ​...
varvarec varvarec  08.04.2020 09:46
ОЧЕНЬ Найдите знаменатель бесконечно убывающей геометрической прогрессии, у которой: 1) b1=3 , S= 3,5 2) S6= 7/8 S 3)b2= -1/2, S=1,6 4)19S=27S3​...
lenaprivet lenaprivet  08.04.2020 09:46
Запиши уравнение, еслиизвестно,что x1,2=​...
sh0d1 sh0d1  08.04.2020 09:46
Укажите допустимые значения переменной в выражении 2х+3/х(х+1)+4/3х​...
Гаргульчик Гаргульчик  08.04.2020 09:46
с задачами Чтобы ликвидировать опоздание на 2 ч, поезд на перегоне в 840 км увеличил скорость, с которой шёл по расписанию, на 14 км/ч. Какова скорость поезда по расписанию?2)Предприниматель...
Ninick Ninick  08.04.2020 09:46
Решить иррациональное уравнение √3х+7=2.5​...
Лизавеликая1111 Лизавеликая1111  08.04.2020 09:46
Катер власна швидкість якого дорівнює 16 км/г, пройшов 36 км за течією і 14 проти течії витративши на весь шлях 3 год. Знайдіть швидкість течії, якщо вона менша від 4 км/г...
RuStAm09 RuStAm09  12.12.2020 02:06
Решите второй вариант по алгебре...
razdor1996Rqzdor razdor1996Rqzdor  12.12.2020 02:06
Даны векторы а{1,3},b=-20{+30},с=2а-1/2b найдите к оординаты и длену векутора с...

Популярные вопросы