35 . докажите, что
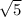
не является рациональным числом.
Другие вопросы по теме Алгебра
Популярные вопросы
- 1. О ком Осип говорит следующее: “А всё он виноват… А отчего? – оттого, что...
3 - 151. Выпишите словосочетания, в которые входят наречия. Над наречиями сокращённо...
2 - Напишите краткое сообщение о происхождении астрологии...
2 - „Правило дев’ятки” регулює правопис: а) усіх слів іншомовного походження;...
1 - 3 предложения о лете на английском...
2 - Across 3.I wear it round my neck. 5.I wear them in my hair. 8.I wear it round...
1 - Клетка, оболочка которой содержит хитин. Вещество, которого нет в растительной...
2 - кто шарит напишите кластер по теме два направления музыкальной культуры 1...
2 - Английский язык 5 класс, задание 4 ( поставь предложения в Present Perfect....
2 - 1.Обозначьте на контурной карте все объекты, которые, на ваш взгляд, характеризуют...
3
Пусть число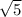 рационально. Тогда
рационально. Тогда 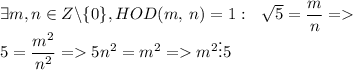
Т.к. 5 - простое, то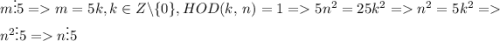 - т.е. и
- т.е. и 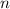 , и
, и 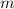 кратны 5, а значит
кратны 5, а значит 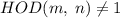 - противоречие.
- противоречие.
А значит предположение неверно, и число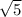 иррационально.
иррационально.
Ч.т.д.