30 ! подробно с решением на !
 \leqslant 0)
Другие вопросы по теме Алгебра
Популярные вопросы
- Написати 6 речень з третьов особов однини...
3 - 4кг яблок и 1 кг груш стоят 98 руб сколько стоит 1 кг яблок...
3 - Опишите в 3-5 предложениях как вы поняли смысл ”стремитесь не...
2 - Выпишите слова с чередующейся гласной в корне косичка, росинка,...
3 - Написать творческую работу успешный человек какой он план: 1.условия...
3 - Нужно я не знаю как сделать. мне нужно на завтра....
1 - A) координаты точек пересечения этого графика с осями координат...
3 - Выразите в метрах 2 км 8600 см 16 дм 34000 мм...
1 - Сколько стоят органы человека на чорном рынке...
1 - Вопросы и к стихотворению если жизнь тебя 1. что, по мнению...
1
Метод рационализации: заменяем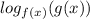 на произведение
на произведение 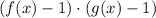 , учитывая ОДЗ .
, учитывая ОДЗ .