3^x+2^x=5^x решить уравнение
Другие вопросы по теме Алгебра
Популярные вопросы
- Объяснить пословицу: будущее принадлежит тем,кто готовится к этому...
2 - Запишите число, составленное из номеров верных утверждений. 1. если перед скобками...
2 - Choose the right tense from he often buys/ is buying flowers for her bill plays/...
3 - Сколько центнеров в 2,92 т, 7 т 6 ц 4 кг, 1 т 2 ц 3 кг...
1 - Напишите рассказ на тему завоевательные походы александра македонского количество...
2 - Мини-сочинение про доброго человека по обществознанию....
3 - Поставити запитання до слова називається...
1 - Данные словосочетание замени глаголом покрывать цветами...
3 - (9 9) 9=0 поставьте плюс или отнять или делить или умножить 9 (9 9)=0...
1 - Как никита относиться к природе в произведении «никита» (платонов)...
2
Корень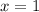 угадывается сразу. Покажем, что других корней нет. Для этого можно было бы изучить функцию
угадывается сразу. Покажем, что других корней нет. Для этого можно было бы изучить функцию 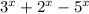 , но она не является монотонной. Вместо этого поделим уравнение на
, но она не является монотонной. Вместо этого поделим уравнение на 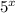 , получив
, получив 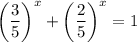 , после чего изучим функцию
, после чего изучим функцию 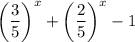 . Она уже очевидно монотонна (как сумма монотонно убывающих), а потому и решение может быть только одно.
. Она уже очевидно монотонна (как сумма монотонно убывающих), а потому и решение может быть только одно.
Показать это можно и просто вычислив производную: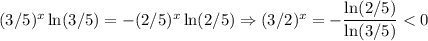 .
.