3) Найдите значение выражения 2хо–уо, если (хо; уо) – решение системы уравнений: y= 2корень(x+3)
y+ 2= |x+2|
Заранее
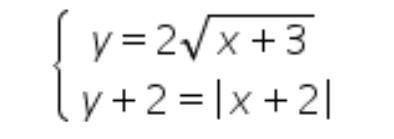
Другие вопросы по теме Алгебра
Популярные вопросы
- Сколько нужно пчел, чтобы поднять грузовик с пинцетами...
1 - Новый год в испании. Прочитай объявление, предположи, кто из ребят запишется...
1 - 3.Выпішыце назвы жывёл, якія адносяцца да класа Ракападобныя: тарантул,...
3 - Для острого угла sin a,cosa и ctga,если tg=1/5 . Решите желательно расписанное...
3 - Task 3 Arrange the words in the correct order. Make sentences using these...
2 - Обрати чинники, що не впливають на швидкість хімічної реакції: а) тиск;...
2 - Определить газовы состав воздуха...
2 - Составьте синквейны, посвящённые персонажам романа Р.Л.Стайна 1) Гейб...
2 - 1.Берілгені : Шешуі : a = 80M Р = ( а + в ) * 2 В = 8м P = P = ? M Жауабы...
1 - Найдите сумму целых решений неравенства x^2+2x меньше или ровно 3...
2
Из второго уравнения системы выражаем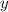 :
:
И подставляем в первое уравнение:
При этом нужно учитывать, что:
Из первого неравенства получаем, что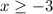 .
.
Во втором неравенстве нужно рассмотреть два случая: при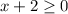 имеем, что
имеем, что 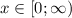 , при
, при 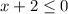 получаем, что
получаем, что ![x \in (-\infty;-4]](/tpl/images/1357/2404/b7715.png) . В итоге
. В итоге ![x \in ( - \infty; -4 ] \cup [0; + \infty)](/tpl/images/1357/2404/808c8.png) .
.
В итоге получаем пересечение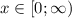 .
.
Учитывая это, возводим обе части полученного ранее уравнения в квадрат и раскрываем модули:
При теоремы Виета получаем, что:
Первый корень не удовлетворяет нас по введенным ограничениям, так что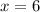 .
.
Найдем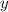 :
:
Получаем, что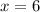 и
и 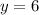 . Эта пара удовлетворяет и первому уравнению, как можно убедиться.
. Эта пара удовлетворяет и первому уравнению, как можно убедиться.
Так что:
Задача решена!
ответ: 6................................