3. катер в 10: 00 вышел из пункта а в пункт в, расположенный в 15 км от а. пробыв в пункте в 1 час 15 минут, катер отправился назад и вернулся в пункт а в 14: 00 того же дня. определите (в км/ч) собственную скорость катера, если известно, что скорость течения реки равна 1 км/ч

время, которое катер был в пути = 14-10-1ч.15мин = 2ч.45мин = 2,75ч

пусть X - скорость катера, тогда время, потраченное на путь из А в В равно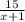 , где 15 - расстояние между А и В, а (x+1) скорость катера по течению.

Время, затраченное на обратный путь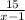 , (x-1) - скорость против течения.

А всего в пути катер был 2,75ч. Составим уравнение

X1=-0.09 - не подходит, т.к. скорость не может быть отрицательной

X2 = 11 км/ч - скорость катера