3*2^(2x)-5*6^x+2*3^(2*x)=0 как решить?
Другие вопросы по теме Алгебра
Популярные вопросы
- Укажіть речення, у якому відокремлена обставина виражена іменником з прийменником....
2 - Ex.1 – Open the brackets, using going to V in written form . 1. He his...
1 - 8. Расположите столицы стран Юго-Западной Азии с юга на север: А Анкара...
3 - Скорочно по физкультуре.Тема Эстафетный бег.1. Какое положение на 2. Какое...
1 - решить 2 и 4 задачи. Заранее огромное...
3 - У реченні «Лінгвістика, або наука про мову, захоплює багатьох студентів»...
1 - Постройте в координатной плоскости прямоугольник с вершинами А(-3,4),В(5,4),С(5,-1),Д(-3,-1)...
2 - Определите тему текста (о чем текст?) «О том, что принято и не принято...
1 - В треугольнике АВС стенка ВС равна 24 см, а углы А и С равны 45° и 60°соответственно....
2 - Чи можна назвати твір Вітька+Галя гумористичним?...
1
Пусть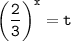 при этом
при этом 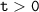 , тогда получим
, тогда получим
Возвращаемся к обратной замене