2x+4y+3z=-10 -x+5y-2z=5 3x-2y+4z=3 методом крамера, 7 задания второй пример
Другие вопросы по теме Алгебра
Популярные вопросы
- О чём произведение Петя Ростов дам...
3 - Сколько грамм оксида магния образуется при взаимодействии 18 грамм...
2 - Сочинение я должна стать храбрее сто слов...
2 - Определи слова для повара из нужных ключевых слов и словосочетаний....
1 - 4 Какими членами предложения являются однородные члены?Красив, наряден...
1 - Один моль одноатомного идеального газа совершает процесс 1-2-3 (см....
2 - История Бернудского треугольника...
3 - пожайлуста.нужно сделать фишбоун на тему рождество ....
2 - надо Рабочий по полу равномерно перемещает груз массой 50 кг, с коэффициентом...
2 - 2. Напишите уравнения реакций горения, расставьте коэффициенты. C4H8...
2
ответ: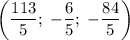
Объяснение:
Решить систему методом Крамера:
Найдем главный определитель системы:
где a, b, c - числовые коэффициенты при x, y, z соответственно.
Найдем определитель разложением по первой строке:
Δ = a₁ · (b₂c₃ - b₃c₂) - b₁ · (a₂c₃ - a₃c₂) + c₁ · (a₂b₃ - a₃b₂)
Вычислим Δ:
Δ ≠ 0 ⇒ система имеет единственное решение.
Для нахождения корней необходимо вычислить еще три определителя:
1. Δх.
Заменим в главном определителе первый столбец на столбец свободных членов (d):
Вычислим Δх:
2. Δy.
Заменим в главном определителе второй столбец на столбец свободных членов (d):
Вычислим Δy:
3. Δz.
Заменим в главном определителе третий столбец на столбец свободных членов (d):
Вычислим Δz:
ответ рассчитывается по формулам:
Найдем корни:
ответ: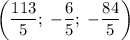
#SPJ1