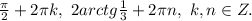2sin(x)+cos(x)=2 тригонометрическое уравнение
Другие вопросы по теме Алгебра
Популярные вопросы
- Задание №5. ответь на вопросы: ( ) 1. Какие животные для кочевников-номадов...
1 - 3) 11Выполните деление (607, 608).483 1607. 1)5)5 252 34)6)812 6:7)о10...
1 - • Past simple Present perfect85671 Put the verbs inbrackets into the...
1 - 2. С анализа перечислитеизменения, которыевызвала Гражданскаявойна...
2 - Замените словосочетание нотки горечи,посторонное на основе управления,синонимичным...
3 - Математика, упростите запись числа...
1 - спам не надо сразу жалоба чисто ответь на 6 вопросов Текст верху и...
3 - Соотнести что к чему относится? ...
3 - перемтр ппралелограма жорианюе 112см видом що одна сторона и 7 разивбильше...
3 - Памагите 8класс английский...
3
2sin x + cos x = 2
Один из
Раскроем скобки, упростим, перенесем в одну часть относительно знака "=":
Делим обе части на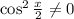
ответ: