2sin^2 (пи/12) + 8cos ^2(пи/8) решить пошагово
Ответы
Понижаем степень по формулам:
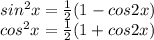
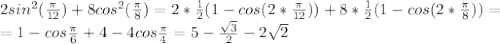
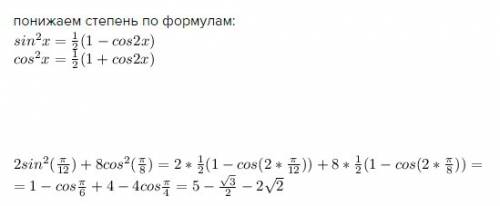
ПОКАЗАТЬ ОТВЕТЫ
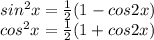
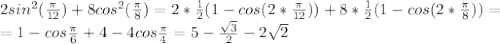
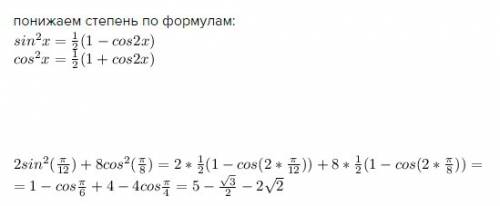
Другие вопросы по теме Алгебра
Популярные вопросы
- Напиши,герои каких книг тебе нравится. почему?...
1 - Расскажи что делает вечером мама.свой рассказ запиши.3 ,4 предложения....
3 - 1)в ателье было 48 м ткани в клетку,а ткани в горошек в 6 раз меньше.вторую...
1 - 1.он в самом омуте живёт,хозяин глубины.имеет он огромный рот,а глазки чуть...
3 - Слово подставив -причастие,деепричастие или...
3 - Почему афинские граждани выбирали стратегом перикла 15 раз?...
2 - Из пакета с кортофелем вес которого 3кг отсыпали 1кг какая часть картофеля осталась...
3 - Для вычисления значений примените правило вычитания суммы из суммы (600++9)...
3 - Составьте с одним из них ра предложение со словами изморозь подземка пурга...
2 - Дроби к знаменателю 60 2/5 5/12 7/15 13/30...
1