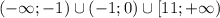2lg(x^2-10x) / lgx^2 < =1 что тут сделать можно? как пропорцию или к общему знаменателю? или вообще что-то иное?
Другие вопросы по теме Алгебра
Популярные вопросы
- Сколько месяцев в году музей «Семёнково» открыт с 10:00 до 19:00 ?варианты...
1 - Вы решили посетить Музей Победы в апреле 2020 года. Изучите расписание...
2 - Составьте в форме таблицы сравнительную характеристику рек Маккензи и...
2 - А.Пушкин ,,Пиковая дама,, 2Какой смысл, по вашему мнению, скрывается за...
3 - Нужен кроссворд на город Лангепас...
3 - Какие оружия были у манголов...
3 - Вставь пропущенное число. 4010 : ___ = 27 (ост...
3 - Проект по литературе Языковая палитра о Слове о Полку Игореве Введение1....
1 - Расположите в хронологической последовательности ароморфозы: 1. возникновение...
3 - решить этот пример (Можно сразу ответ)...
1
Можно воспользоваться свойством логарифма:
Вот что у меня получилось:
последние три неравенства системы - область определения.
Решим их, получим:
x принадлежит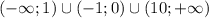
Решим исходное неравенство:
x(x-11)=0
x=0
x=11
+ - +
--------'---------'-------->
0 11
x принадлежит![(-\infty;0]\cup[11;+\infty)](/tpl/images/0049/5083/ee8fe.png)
Учтем область определения:
х принадлежит