25^x-(2a+1)*5^x+a^2+a=0
решить
Другие вопросы по теме Алгебра
Популярные вопросы
- 2+5*2=? ПОЧЕМУ КАЛЬКУЛЯТОР ГОВОРИТ ЧТО ОТВЕТ 12?...
2 - Информация и информационные процессы, пересказ...
2 - 4. Какое из чисел больше : -5,419* -5,42а) -5,419 b) -5,42 с) равны...
3 - Как ведёт себя Ахилл выслушав Приама? О чём говорят его жесты?...
2 - 29. Назовите все отрезки изображеннные на рис...
1 - 2. АС- діагональ квадрата ABCD. Обчисліть величину кутів трикутника ADC...
2 - Индивидуальная работа 1. Найти значение выражения: 1 1) а+ 4,6 при а = -10,8;...
3 - F(x)=4x+x^3/21-3x Четная/нечетная/ни четная, ни нечетная....
3 - Розв язати хімічні рівняння...
3 - При каких значениях переменной имеет смысл выражение 15−2r12−−−−−−−√? Выбери...
2
ответ:a>0: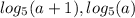 ; a=0:x=0
; a=0:x=0
Объяснение:
и ограничения на a:
a>0
Если же a=0: