249. Вычислите площадь ромба, высота которого равна 3, а острый угол в 2 раза меньше тупого.
Другие вопросы по теме Алгебра
Популярные вопросы
- Правила перехода игроков во время игры в волейбол....
3 - Наибольшим зональным природным комплексом является: А) материк Б)...
3 - Мне нужно исправить ошибки в коде програма Pascal Program massiv;...
2 - Земли, которые отказывались платить дань....
1 - объясните, что означает понятие Керамик и какие вазы называли чернофигурными...
2 - Ускорение свободного падения на некоторой планете g=12 м\с2 первая...
3 - Задание №2. Выполните морфологический разбор местоимения: Из первого...
1 - Выполнить действия,можно по действиям......
1 - Синквейн на тему ««Концерт как музыкальный жанр»...
2 - Вычислить наиболее удобным...
1
P=4a = 4*2=8
Объяснение:
острый угол = 180- тупой угол
H=√3 . пусть х острый угол , тогда тупой 2x ,
3x=180
x=60 гр , значит углы равны 60 и 120 градусов
Опустим высота получим прямоугольный треугольник
√3/sin60=a где "а" сторона ромба
a=2
P=4a = 4*2=8
Высота ромба равна h=BH=3 , h ⊥ a или BH⊥AD .
Обозначим сторону ромба через а , острый угол - через х° .
Тогда тупой угол равен 2х° . Так как сумма углов, прилежащих к одной и той же стороне ромба, равна 180°, то х°+2х°=180° , 3х°=180° ,
х°=60° - острый угол
Рассмотрим ΔАВН , ∠АНВ=90° , а=h/sinx° ,
АВ=BH/sin60°=3/(√3/2)=2√3 .
Площадь ромба равна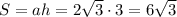 .
.
Или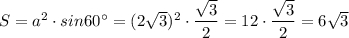 .
.