20б. решение вероятностных с комбинаторики. 1. бросают две монеты - белую и желтую.найти вероятность того, что: 1) на обеих монетах появилась решка. 2. саша(с), варя(в) и гена(г) случайным образом заняли очередь в школьный буфет. найти вероятность того, что образовалась очередь в следующем
порядке: 1) свг 2) вгс 3) гсв или гвс 4) свг или всг 3. бросают два игральных тетраэдра- белый и зеленый, грани которых пронумерованы числами от 1 до 4. найти вероятность того, что появятся: 1) на белом тетраэдре 3 очка, на зеленом- 4 очка; 2)на белом тетраэдре 1 очко,на зеленом-2 очка; 3)на
белом тетраэдре четное число очков, на зеленом- 2 очка; 4) на белом тетраэдре нечетное число очков, на зеленом-3 очка 5)на белом тетраэдре 2 или 4 очка; 6) на зеленом тетраэдре 1 или 3 очка; 7)очки, сумма которых равна 2; 8) очки, сумма которых равна 8; 9) очки, сумма которых равна 7; 10)
очки, сумма которых равна 3; 11)очки, произведение которых равно 12; 12)очки, произведение которых равно 2; 13)очки, произведение которых равно 4; 14)очки, произведение которых равно 6;

Ответы

beyn1oyc4cd 10.10.2020 01:20

Вероятность того, что на одной монете появится решка — 1/2

, шанс, что на обеих сразу — $(1/2)\cdot(1/2)=1/4$ .Возможны 3!=6

комбинаций, тогда шанс, что выпадет конкретная комбинация — 1/6

. Тогда шанс, что выпадет СВГ — 1/6

, ВГС —

, ГСВ или ГВС — 2/6=1/3

, СВГ или ВСГ — 2/6=1/3

.Шанс, что выпадет конкретное число — 1/4

, что выпадут на обоих сразу — $(1/4)\cdot(1/4)=1/16$ , тогда:
$(1/4)\cdot(1/4)=1/16$ $(1/4)\cdot(1/4)=1/16$ Четных

, поэтому $(2/4)\cdot(1/4)=2/16=1/8$ Нечетных

, поэтому $(2/4)\cdot(1/4)=2/16=1/8$ 2/4=1/2

Сума будет

, только при

, тогда $(1/4)\cdot(1/4)=1/16$ Сума будет

, только при

, тогда $(1/4)\cdot(1/4)=1/16$ Сума будет

, только при

или

, тогда $((1/4)\cdot(1/4))+((1/4)\cdot(1/4))=(1/16)+(1/16)=2/16=1/8$ Сума будет

, только при

или

, тогда $((1/4)\cdot(1/4))+((1/4)\cdot(1/4))=(1/16)+(1/16)=2/16=1/8$ Произведение будет

, только при

или

, тогда $((1/4)\cdot(1/4))+((1/4)\cdot(1/4))=(1/16)+(1/16)=2/16=1/8$ Произведение будет

, только при

или

, тогда $((1/4)\cdot(1/4))+((1/4)\cdot(1/4))=(1/16)+(1/16)=2/16=1/8$ Произведение будет

, только при

, тогда $(1/4)\cdot(1/4)=1/16$ Произведение будет

, только при

или

, тогда $((1/4)\cdot(1/4))+((1/4)\cdot(1/4))=(1/16)+(1/16)=2/16=1/8$

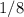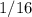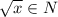Можно было сказать, что произведение и сумма состоят из двух чисел, если их можно поменять местами, то шанс — 1/8 , иначе — 1/16 . То есть если мы говорим о произведении равном то если $\sqrt x\in N$ , если сумме — если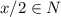 $x/2\in N$

ПОКАЗАТЬ ОТВЕТЫ

smail550 21.01.2024 19:43

1) Вероятность того, что на обеих монетах появилась решка может быть найдена с помощью комбинаторики.

В данном случае мы имеем 2 монеты - белую и желтую. У каждой монеты есть 2 возможных исхода: решка (Р) или орел (О). Таким образом, общее число исходов равно 2 * 2 = 4.

Задача требует найти вероятность появления решки на обеих монетах. В данном случае, это означает, что нужно найти количество комбинаций, где на обеих монетах выпал решка, и разделить его на общее количество возможных комбинаций.

Вероятность равна количеству благоприятных исходов, деленных на общее количество исходов: P(решка на обеих монетах) = количество благоприятных исходов / общее количество исходов.

Количество благоприятных исходов равно 1 (так как есть только 1 комбинация, где на обеих монетах выпал решка: Р-Р).

Общее количество исходов равно 4.

Таким образом, вероятность того, что на обеих монетах появилась решка, равна 1/4.

2) Вероятность того, что образовалась очередь в следующем порядке:
а) СВГ (где С - Саша, B - Варя, Г - Гена)

Рассмотрим все возможные комбинации:

СВГ, СГВ, ВСГ, ВГС, ГСВ, ГВС.

В данной задаче количество благоприятных исходов равно 1 (СВГ), а общее количество исходов равно 6.

Таким образом, вероятность того, что образовалась очередь СВГ, равна 1/6.

б) ВГС

Аналогично, количество благоприятных исходов равно 1 (ВГС), а общее количество исходов равно 6.

Таким образом, вероятность того, что образовалась очередь ВГС, равна 1/6.

в) ГСВ или ГВС

Количество благоприятных исходов равно 2 (ГСВ и ГВС), а общее количество исходов равно 6.

Таким образом, вероятность того, что образовалась очередь ГСВ или ГВС, равна 2/6 = 1/3.

г) СВГ или ВСГ

Количество благоприятных исходов равно 2 (СВГ и ВСГ), а общее количество исходов равно 6.

Таким образом, вероятность того, что образовалась очередь СВГ или ВСГ, равна 2/6 = 1/3.

3) Вероятность выпадения определенной комбинации на двух игральных тетраэдрах может быть найдена аналогичным образом.

а) На белом тетраэдре 3 очка, на зеленом - 4 очка

У каждого тетраэдра 4 грани, поэтому общее количество возможных комбинаций равно 4 * 4 = 16.

Количество благоприятных исходов равно 1 (3 на белом тетраэдре и 4 на зеленом тетраэдре).

Таким образом, вероятность того, что на белом тетраэдре выпадет 3 очка, а на зеленом - 4 очка, равна 1/16.

б) На белом тетраэдре 1 очко, на зеленом - 2 очка

Аналогично, количество благоприятных исходов равно 1 (1 на белом тетраэдре и 2 на зеленом тетраэдре).

Таким образом, вероятность того, что на белом тетраэдре выпадет 1 очко, а на зеленом - 2 очка, также равна 1/16.

в) На белом тетраэдре четное число очков, на зеленом - 2 очка

Аналогично, количество благоприятных исходов равно 2 (2 и 4 на белом тетраэдре и 2 на зеленом тетраэдре).

Таким образом, вероятность того, что на белом тетраэдре выпадет четное число очков, а на зеленом - 2 очка, равна 2/16 = 1/8.

г) На белом тетраэдре нечетное число очков, на зеленом - 3 очка

Количество благоприятных исходов равно 2 (1 и 3 на белом тетраэдре и 3 на зеленом тетраэдре).

Таким образом, вероятность того, что на белом тетраэдре выпадет нечетное число очков, а на зеленом - 3 очка, равна 2/16 = 1/8.

4) На белом тетраэдре 2 или 4 очка

Количество благоприятных исходов равно 2 (2 и 4 на белом тетраэдре), а общее количество исходов равно 4 * 4 = 16.

Таким образом, вероятность того, что на белом тетраэдре выпадет 2 или 4 очка, равна 2/16 = 1/8.

5) На зеленом тетраэдре 1 или 3 очка

Аналогично, количество благоприятных исходов равно 2 (1 и 3 на зеленом тетраэдре), а общее количество исходов равно 4 * 4 = 16.

Таким образом, вероятность того, что на зеленом тетраэдре выпадет 1 или 3 очка, равна 2/16 = 1/8.

6) Очки, сумма которых равна 2

Количество благоприятных исходов равно 1 (1 + 1), а общее количество исходов равно 4 * 4 = 16.

Таким образом, вероятность того, что сумма очков будет равна 2, равна 1/16.

7) Очки, сумма которых равна 8

Количество благоприятных исходов равно 1 (4 + 4), а общее количество исходов равно 4 * 4 = 16.

Таким образом, вероятность того, что сумма очков будет равна 8, также равна 1/16.

8) Очки, сумма которых равна 7

Количество благоприятных исходов равно 2 (3 + 4 и 4 + 3), а общее количество исходов равно 4 * 4 = 16.

Таким образом, вероятность того, что сумма очков будет равна 7, равна 2/16 = 1/8.

9) Очки, сумма которых равна 3

Количество благоприятных исходов равно 1 (1 + 2), а общее количество исходов равно 4 * 4 = 16.

Таким образом, вероятность того, что сумма очков будет равна 3, равна 1/16.

10) Очки, произведение которых равно 12

Количество благоприятных исходов равно 2 (3 * 4 и 4 * 3), а общее количество исходов равно 4 * 4 = 16.

Таким образом, вероятность того, что произведение очков будет равно 12, равна 2/16 = 1/8.

11) Очки, произведение которых равно 2

Количество благоприятных исходов равно 1 (1 * 2), а общее количество исходов равно 4 * 4 = 16.

Таким образом, вероятность того, что произведение очков будет равно 2, равна 1/16.

12) Очки, произведение которых равно 4

Количество благоприятных исходов равно 2 (1 * 4 и 2 * 2), а общее количество исходов равно 4 * 4 = 16.

Таким образом, вероятность того, что произведение очков будет равно 4, равна 2/16 = 1/8.

13) Очки, произведение которых равно 4

Количество благоприятных исходов равно 3 (1 * 1, 1 * 2, 2 * 1), а общее количество исходов равно 4 * 4 = 16.

Таким образом, вероятность того, что произведение очков будет равно 4, равна 3/16.

14) Очки, произведение которых равно 6

Количество благоприятных исходов равно 2 (1 * 6 и 2 * 3), а общее количество исходов равно 4 * 4 = 16.

Таким образом, вероятность того, что произведение очков будет равно 6, равна 2/16 = 1/8.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра