20 1) найдите корни биполярного уравнения2) решите турист проплыл на лодке против течения реки 25 км,а возвратился на плоту.в лодке он проплыл на 10 часов меньше чем на плоту. найдите скорость течения реки если скорость лодки в стоячей воде равна 12 км/ч.​

1 Решила методом замены

2 Взяла за х скорость речки

1)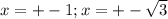 2) 2 км/ч

Объяснение:

1) Не биполярное, а биквадратное, Сделаем замену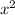 = t, тогда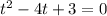

                D = 4*4 - 4 * 3 = 4 = 2*2

                t1 = (4-2)/2 = 1

                t2 = (4+2)/2 = 3

Делаем обратную замену:

                =1                                       =3

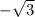                x = -1; x = 1;                         x=;x=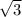

2) Пусть x - скорость течения Так как обратно он смог вернутся на плоту, то тогда он плыл по течению, значит изначально он плывет против течения со скоростью 12 - x, а затратил он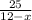 часов.

Плывя на плоту он потратил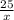 часов, но еще из условия известно, что время на лодке = время на плоту - 10, т.е

Домножим на x(12-x):

Раскроем скобки:

Перенесём в правую часть и приведем подобные слагаемые:

скорость течения не может быть больше скорости лодки