, 2 ВАРИАНТ НАДО РЕШИТЬ НЕ КОНТРОЛЬНАЯ А ДЗ НА ДОСКЕ НАПИСАЛИ, ПОЧЕМУ БАНЯТ ТО
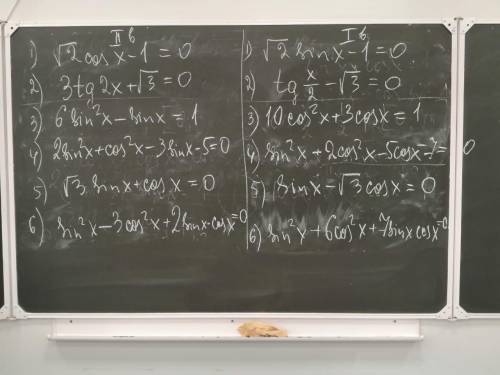
Другие вопросы по теме Алгебра
Популярные вопросы
- Как решить в столбик деление 896 разделить на 8 768 разделить на 3...
2 - Во сколько раз увеличивается значение цифры 3 от разряда единиц к разряду сотен?...
3 - Сочинение на тему почему мне будет интересно изучать науку зоология...
2 - Впрямоугольной трапеции боковые стороны равны 17 и 15 а меньшее основание в два...
2 - Звукобуквенный анализ слова молодая...
3 - Впервый час водитель проехал 68км что составило 40% от длины всего пути, во второй...
2 - Деревянный брусок движется равномерно по поверхности демонстрационного стола под...
3 - Чем наблюдение отличаеться от экспиремента...
3 - Как вы считаете, отразились ли суровые природные условия на характере россиян?...
2 - Мама старше дочери на 22 года, а маме и дочери вместе 74 года. сколько лет дочери...
2
1
2
3
4
5
6
везде n принадлежит Z.