2. Среди трех данных функций укажите - какая из этих функций является первообразной и производной: а) f (х) = 1/х2
g (х) = -1/х
h (х) = -2/х3
б) f (х) = 1
g (х) = х + 2
h (х) = х2 + 2х
Другие вопросы по теме Алгебра
Популярные вопросы
- Выписать из р-за В.П.Астафьева Конь с розовой гривой 5 архаизмов и диалектизмов(вместе)....
1 - При трении стеклянной палочки о шёлк палочка приобрела заряд q=5.76 мКл....
3 - УМОЛЯЮ! НА 65 СЛОВ РАССКАЗ ОТ ЛИЦА ГЕРОЯ...
3 - Реши по действием 204*85+(10000-1975):25 если не по действием ОТМЕЧУ КАК...
1 - 7. Установите соответствие между выделенными в предложенияхсловами и их...
1 - Изобретение лук и стрел началу войны да или нет ребят плз...
3 - Это синтаксический разбор слова, но что может обозначать эти знаки например...
1 - 3. 4. Атом Феруму містить електронів:...
3 - Lasa bigIt has small ears/a mouth.63Complete the telephone talk.Hello....
3 - Сочинение на тему Любовь как открытие мира в рассказе Голубое и зелёное...
1
Производная функции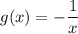 равна
равна 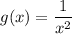 .
.
Первообразная функции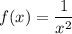 равна
равна 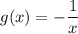 .
.
Первообразная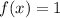 для функции
для функции 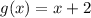 .
.
Производная функции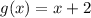 равна
равна 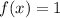 .
.