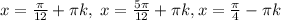2 sin((п/4)-x)=cos(3x-(п/4))
Другие вопросы по теме Алгебра
Популярные вопросы
- Яким реактивом відкривають іон Na+, при яких умовах?...
2 - Закончите уравнение окислительно-восстановительной реакции KСlO3...
2 - АВС и A1, B1, C1 - подобные треугольники. Найдите отношение B1C1/BC?...
1 - Спишите предложение. Сделайте синтаксический разбор. Страна,...
1 - Исправить предложения имеется в продаже пустая коробка надо прихлопнуть...
3 - Напишіть правила проведення інструктажів з техніки безпеки. використання...
2 - Тапсырма 2. Сұраққа жауап беріңіз? 1. Сызықтық программа дегеніміз...
3 - к истории древней Греции относиться: 1) Долговой камень 2)Учение...
2 - Здійснити орфографічно-пунктуаційне редагування тексту. Накреслити...
3 - 2 метил 3 этил нонан формуласын жаз.пентан три ол формуласын жаз.1.2.4....
3
Пусть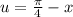 ;
;
Рассмотрим два случая:
1)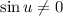
Воспользуемся формулой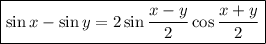 ;
;
_____________________________________________________
Здесь ее краткий вывод:
Пусть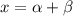 , а
, а  ; Такие числа легко найти:
; Такие числа легко найти: 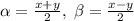 ;
;
Получаем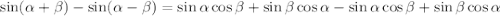
В итоге ;
;
_____________________________________________________
Итак,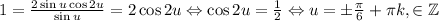
Откуда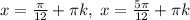
2)
Тогда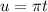 и
и 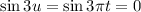 . То есть получили равенство.
. То есть получили равенство.
ответ: