1. Алгебра
  2. 2.найдите угловой коэффициент

2.найдите угловой коэффициент касательной к графику f(x),проведенной к точке графика с абсциссом x0: a)f(x)=sin x +2^x0= \pi б)fx)=x^2+4x-5^x0=1

itsnastyad itsnastyad    1   30.08.2019 17:40    0

Ответы
ZoeK ZoeK  31.08.2020 23:58
Угловой коэффициент касательной к графику функции равен значению производной в точке касания:
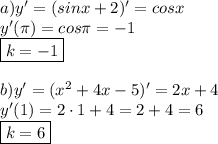
a) y' = (sinx + 2)' = cosx \\
y'( \pi ) = cos \pi = -1 \\
\boxed{k = -1} \\ \\
b) y' = (x^2 + 4x - 5)' = 2x + 4 \\
y'(1) = 2 \cdot 1 + 4 = 2 + 4 = 6 \\
\boxed{k = 6}

2.найдите угловой коэффициент касательной к графику f(x),проведенной к точке графика с абсциссом x0:
ПОКАЗАТЬ ОТВЕТЫ
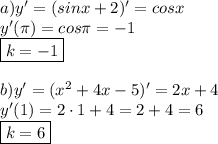
Другие вопросы по теме Алгебра
привет6365 привет6365  21.05.2020 12:21
Сумма цифр двузначного числа в 4 раза меньше самого числа. если это число уменьшить на 9, то число будет в 3 раза больше суммы цифр. Найдите это число)​...
Ciropchik Ciropchik  21.05.2020 12:22
Выполните умножение дробей:...
HelpmeTT HelpmeTT  21.05.2020 12:22
Помагите пожайлуста мне надо...
Illia1Z Illia1Z  21.05.2020 12:22
Решите через дискриминант....
banana92 banana92  21.05.2020 12:22
A(0;5), B(5;-7).AB Найдите длину отрезка...
Narine10 Narine10  21.05.2020 12:22
Щоб ліквідувати запізнення на 1 годину, поізд на перегоні 720 км збільшив швидкість, з якою іхав за розкладом, на 10 км загодину. Яка швидкість поізда за розкладом?6.Катер, швидкість...
arifmametov1 arifmametov1  25.02.2021 16:56
решить, не могу разобраться...
dariaAppp dariaAppp  25.02.2021 16:56
Найдите sin(a+в) и cos(а-в), если sina = 0,6 и cosв = 0,8 0,5pi =a =pi, 1,5pi =в =2pi...
elena563 elena563  25.02.2021 16:57
Найдите значение выражения 5ctg(a+7П/2)/4tg(a+3П) если а=5П не очень понимаю как решить...
KsushaTrefilova KsushaTrefilova  25.02.2021 16:57
Заданы комплексные числа z1=1-i и z2=1-i а) Вычислите w=2z1/z2 +z1 где z1*- число, сопряжённое числу z1. ответ запишите в алгебраической форме. b) Найдите модуль числа w.​...

Популярные вопросы