2.3 Решите задачу с дробно-рационального уравнения: Турист проплыл на лодке 3 км по течению реки и 2 км против течения реки за 30
минут.
Найти скорость лодки в стоячей воде, если скорость течения реки 2км/ч.
Другие вопросы по теме Алгебра
Популярные вопросы
- Тарас и бульба. напишите сочинение (350 слов) на тему что значит отчизна для любого...
2 - Сочинение на тему характеры жанны и её мужа в рассказе л.н. толстого бедные люди...
2 - Назовите эмоциональные и рациональные товары. т. е. каждый товар должен быть и...
3 - В295.какими словами и выражениями из данных ниже можно обьяснить выделенные фразеологизмы...
1 - Определите вид связи в словосочетании по голубом небу ...
1 - Вкакой координатной четверти может находится угол, если...
1 - 308a. прочитайте текст.когда (то) один публицист заметил, что все человечество...
2 - 1) à) p(a + b); á) −y(k + c); â) a(k + c − 5); ã) −x(a − b + 1); 2) a) 7a3(3 −...
3 - Отметьте слова с буквой и после ц * станц..я...
2 - Запишите уравнение окружности с центром в m радиуса r,если m(-3; 2),r=2. б)проходит...
2
30 мин =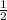 часа
часа
Уравнение:
10 км/ч - скорость лодки в стоячей воде.
ответ: 10 км/ч