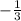(2^2 + 1)(2^4 +1)(2^8 +1)(2^16 + 1)(2^32 + 1)(2^64 + 1) - 1/3 • 2^128
Другие вопросы по теме Алгебра
Популярные вопросы
- Большой круг кровообращения — это путь крови от...
3 - В дыхательных путях происходит согревание воздуха, так как...
1 - Артериальная кровь у человека превращается в венозную в...
2 - Почему кровь не может попасть из желудочка в предсердие?...
1 - Артериальная кровь у человека в момент сокращения миокарда поступает...
2 - Укажите последовательность процессов, происходящих в сердце в течение...
1 - Автоматия сердца человека связана с импульсами, которые возникают...
3 - Пульсовые колебания стенок артерий возникают при сокращении...
2 - Давление крови на стенки сосудов создается силой сокращений...
2 - Какая часть кости является кроветворным органом?...
1
Вывод: все выражение равно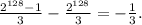
ответ: